Refinement in Specware is a way of saying that one entity can be represented in terms of another; thus it is the main mechanism for describing an implementation. When we wish to implement one structure in terms of another, we build a refinement between the corresponding two specifications. This specification must identity each element of the first specification (the source) in terms of a corresponding element in the second (the target). The correspondence must be such that every property of the source specification maps into a property of the target. Typically, the source specification is the more abstract, while the target is closer to a computational framework.
For example, suppose we want to build an implementation of our theory of plane geometry. Suppose further that we have a theory of real numbers. (In fact, a theory of real numbers already exists in the Specware library.) Then we may use the basic idea of Cartesian geometry: each point may be represented by a pair of real numbers. A line segment, then, may be represented as a pair of pairs of reals, and so forth.
A refinement must identify each element in the source specification
with an element in the target. For example, the refinement of the
specification SEGMENT for a line segment into the reals maps a
line segment s with (distinct) endpoints 
and 
into a pair
of pairs of reals, 
and 
one pair for each
endpoint:
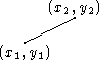
The perpendicular relation between two line segments s and s' will be mapped into a relation on the reals. From Cartesian geometry, we know that this relation holds if one slope is the negative reciprocal of the other:
In this figure, one segment has slope 2, the other, -1/2:
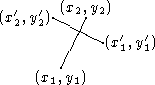
Or, equivalently (cross-multiplying), the segments are perpendicular if::
(The latter form is preferred because it works even in the
case in which the line segments are vertical or horizontal; the
original form involves dividing by zero if, say 
.)
The equal-length relation on line segments will be mapped into a relation on the reals that uses the Pythagorean theorem to test if the following segments s and s' are of equal length:
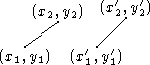
These segments have equal length if:
In general, in a refinement, every concept in the source theory is paraphrased in terms of concepts in the target theory.