The colimit is the fundamental mechanism for composition in Specware. It can be used to compose any specifications, which, as we have mentioned, can represent problem statements, theories, architectures, or programs. The colimit can also be used to compose refinements; refinement is the basic implementation mechanism.
The fact that specifications can be composed via the colimit allows us to build specifications by combining simpler components modularly, just as systems can be composed from simpler modules. If we build theories from components whose correctness has been established, this gives us greater confidence in the composed theory.
The hardest part of composing two entities of any kind is to say how they are to interact. Although sometimes we compose entities that are unrelated, this is unusual. There may be many ways to compose the same two entities, depending on how they are to be related. In Specware, we indicate how specifications are to be composed by identifying what elements they have in common.
For instance, in the Specware theory of plane geometry, we might try to specify a square by saying that it is a rhombus (an equilateral quadrilateral) that is also a rectangle. The specification RHOMBUS for a rhombus will be built on the specification QUAD for a quadrilateral and will also contain the additional axiom that any two sides are of equal length.
To compose RHOMBUS and RECT, we must indicate the elements they have in common that are to be identified. In this case, we want to identify the shared common subspecification QUAD. So, to compose the two specifications, we must identify this shared component.
The fact that one specification may be regarded as a part of another is indicated by the existence of a morphism, a kind of mapping, between them. For instance, the fact that QUAD may be viewed as a part of RHOMBUS is exhibited by the existence of a morphism
![]()
This morphism asserts, in particular, that the four sides of the quadrilateral are the same as the four sides of the rhombus. It is a very simple morphism, since RHOMBUS is built by extending QUAD, but in general there may be many morphisms between the same two specifications.
The morphism
![]()
similarly shows how the notion of a quadrilateral may be viewed as part of the notion of rectangle. Together, these two morphisms indicate how the notions of rhombus and rectangle are to be composed: the notions of quadrilateral contained in each of them are to be identified.
To specify the squares, then, we first form a diagram of the two morphisms:
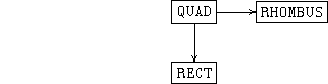
The result of this operation is the specification SQUARE in a diagram that looks like this:
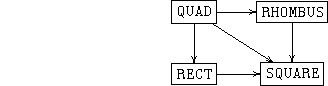
The specification SQUARE combines the elements and properties of all three component specifications, identifying those that are linked by morphisms in the given diagrams. Thus SQUARE combines the notions of a rhombus and a rectangle, and identifies the shared notion of a quadrilateral; the four sides of the rhombus are identified with the four sides of the rectangle. SQUARE contains an axiom that states that any two sides of a square are equal--this axiom is inherited from the specification RHOMBUS; it also contains an axiom that states that adjacent sides of a square are perpendicular--this is inherited from the specification RECT.
It would be possible form a colimit of RHOMBUS and RECT without identifying the common subspecification QUAD. In this case we would obtain the specification R-AND-R in the diagram
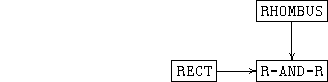
This specification will describe two separate figures, one a rhombus and the other a rectangle. Because we have not indicated that they are to share any structure, we do not combine features of the rhombus and rectangle into a single figure. We could also specify other compositions of rhombus and rectangle, such as a figure in which the rhombus and rectangle share a side or two.
It is possible, unfortunately, to use the colimit to compose correct components to form an inconsistent composition. For example, we might compose a specification for an equilateral triangle with a specification for a right triangle--an inconsistency. Specware has mechanisms for detecting inconsistencies after the fact--subtle inconsistencies may be difficult to observe by casual inspection.
In software development, the colimit is ubiquitous. The composition of two programs and the join of two databases are both examples of colimits. Within Specware itself, the colimit allows greater modularity in the formulation of theories. To specify a set of natural numbers, we need to compose two specifications, one for a set of abstract elements and the other for natural numbers. In some formal-method environments, to compose them requires editing files of axioms--a messy business. In Specware, we simply form a colimit of the diagram

In this way, we can formulate separate theories for sets and natural numbers independently, and combine them subsequently.
Similarly, in specifying a transportation scheduling system, there are two separate components, RESOURCE and TASK (among others). RESOURCE specifies entities such as ships and planes for carrying cargo; TASK specifies particular transportation tasks, such as moving a certain cargo from one place to another before a certain time. These entities have common subspecifications CAPACITY, which specify the available cargo capacities of the ships and planes and the required capacities for the particular transportation tasks, respectively. By forming a colimit, we can compose RESOURCE and TASK, indicating that the identical subspecifications CAPACITY in each are to be identified:
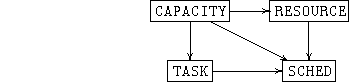
By identifying the common subspecifications CAPACITY, we ensure that the capacity available in the resource agrees with the capacity required for the task. The components RESOURCE and TASK can then be refined independently; Specware will reject refinements that are incompatible.