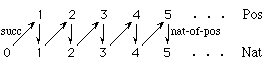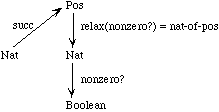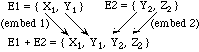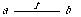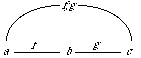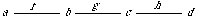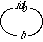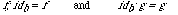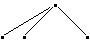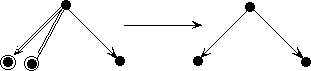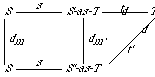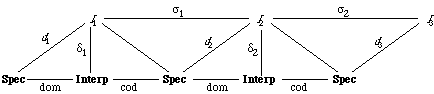Introduction
This document describes the language of the SpecwareTM system. Specware is a system for the specification and formal development of software.
Specware may be regarded as a system for the construction, combination, and manipulation of specifications. There are many levels of specification in Specware. Some describe the ultimate purpose of the target software in abstract terms, some describe the properties and operations of various data structures, and others describe the details of a language-dependent implementation. Domain theories are Specware specifications, and the system has sophisticated facilities for building task-oriented theories from more general ones.
A basic operation in Specware is refinement (also called interpretation), the passage from high-level task-descriptive specifications to low-level implementation-oriented specifications, and ultimately to code generation. This process involves the design of algorithms and the selection of data structures, as well as the generation of code. While mechanical aspects of this task are automated, it is not the intention of Specware to replace the human designer, but rather to support and facilitate the best software-development practices and to ensure that correctness is maintained at each stage in the development of large software systems.
This document is organized as follows. Part I describes the specification constructs in Slang, the Specware language. Section 1 describes basic specifications, which are formed by explicitly providing their constituent sorts, operations, and axioms. Section 2.1 is a brief overview of specification-building operations, which construct new specifications from simpler ones, using morphisms and diagrams, described in Section 2.2. With that background, the specification-building operations--translate, import, and colimit--are described in detail in Section 3.
Part II describes the constructs in Slang for the stepwise refinement of a specification into an implementation. Section 4 gives an overview of the conceptual basis for refinement. Section 5 describes the associated language concepts, interpretations and interpretation morphisms, and how these concepts support the stepwise-refinement process.
Part III contains the appendices, which provide an overview of names in Slang, a BNF grammar for Slang, a table of Slang terms, some sample specifications and interpretations, and an index.
Specware is a visual language, in the sense that there are certain operations that can best be performed and understood in terms of the system's graphical facilities. There is a separate document that details how to interact with the Specware system.
The specifications and interpretations given in this manual are simplified for pedagogical purposes. The actual specifications in the Specware library are accessible via a Specware web page.
Part I Specification Constructs in Specware
Slang, the Specware language, includes constructs for building specifications and their refinements. Refinements are described in Part II; in this part, we describe the specification concepts of Slang:
- specification: A description of an intention, a theory, a data structure, or a program.
- morphism: A mapping between specifications that describes how one specification can be viewed as a part of the other.
- diagram: A graph that indicates how various specifications are to be combined.
- specification-building operation: An operation for building new specifications by combining other, more elementary specifications.
Rather than constructing huge monolithic specifications, it is to our advantage to build them up from many small basic ones. There are several operations for combining specifications in Specware; the most important is the colimit. Before we can use the colimit operation to combine specifications, we must indicate how they are to be related. This is achieved by exhibiting morphisms between them. The colimit operation is applied to a diagram of specifications linked by morphisms.
In Part II we shall discuss how to combine morphisms to build a refinement, a transformation of specifications, which can be used for the selection of data structures and the implementation of software.
1 Basic Specifications
Specifications are the fundamental objects in Slang, the Specware language, and are used to describe domains, data structures, and programs, at multiple levels. In general, a specification is viewed as a presentation or description of a theory. Each specification conveys two pieces of information:
- legal sentences: The set of strings of symbols that are within the language of the theory.
- valid sentences: The subset of the legal sentences that are valid in the theory.
Both sets are infinite, but the specification itself is a finite expression that describes these infinite sets.
Specifications are either given directly as basic specifications or constructed via specification-building operations. This section introduces basic specifications; Section 3 describes specification-building operations.
A full BNF description of the syntax of a specification appears in the appendix; in the text, we give only informal descriptions of syntax. A basic specification consists of a set of specification elements. (In the BNF description of Slang these are called development-elements.) Not all of these elements need appear, and the order of appearance of the elements is irrelevant. We discuss each of these specification elements subsequently in separate subsections.
We distinguish between elements that describe the syntactically legal sentences and those that describe the semantically valid sentences. The legal sentences are described by providing a signature, a presentation of the sorts of objects and operations the theory deals with. Elements that describe the signature are:
- sort: A declaration of the classes of objects discussed by the specification. Each specification has a built-in sort
Boolean, which contains two objects, denoted by true and false, and which is not mentioned explicitly in the specification.
- operation: A declaration of named constants that denote objects, functions, and predicates, of specified sorts. A specification also has a number of built-in operations, such as logical connectives, which are not mentioned explicitly.
-
- sort axiom: An assertion of the equivalence between a primitive sort and a constructed sort. A primitive sort is one that appears explicitly in a sort declaration; a constructed sort is obtained by applying sort-constructor functions to primitive sorts.
spec NAT-BASIC is
sorts Nat, Pos
const zero : Nat
op nonzero? : Nat -> Boolean
definition of nonzero? is
axiom (iff (nonzero? x)
(not (equal x zero)))
end-definition
sort-axiom Pos = Nat | nonzero?
op nat-of-pos : Pos -> Nat
definition of nat-of-pos is
axiom (equal nat-of-pos (relax nonzero?))
end-definition
op succ : Nat -> Pos
axiom (nonzero? (nat-of-pos (succ x)))
axiom succ-is-one-to-one is
(implies (equal (succ x)(succ y))
(equal x y))
constructors {zero, nat-of-pos} construct Nat
constructors {succ} construct Pos
theorem (fa (x : Pos)
(ex (y : Nat)
(equal x (succ y))))
end-spec
Figure 1: Basic Specification for the Nonnegative Integers
Example 1.1 Basic Nonnegative Integers.
To illustrate the discussion throughout this section, we present in Figure 1 a simple specification for the nonnegative integers. (A more complete specification for the nonnegative integers, which builds on this one, will be given in an appendix, Section D on page 158. The specification NAT-BASIC contains two explicit primitive sorts, Nat and Pos, denoting the nonnegative integers and the strictly positive integers respectively; it also contains the implicit built-in sort Boolean .
The constant declaration
const zero : Nat
says that zero stands for an object of sort Nat. The operation declaration
op nonzero? : Nat -> Boolean
stipulates that the operation nonzero? is a predicate on elements of sort Nat; a predicate is a boolean-valued operation. (Although we often end predicate symbols with a question mark, it is not required.) The sort axiom
sort-axiom Pos = Nat | nonzero?
asserts that the primitive sort Pos is equivalent to a constructed sort Nat | nonzero? (which is the subsort of elements of sort Nat that satisfy the predicate nonzero?).
Elements of a specification that describe the subset of valid sentences are:
- axiom: A logical sentence that is asserted to hold for all the objects and functions discussed by the specification.
- definition: A set of axioms that does not restrict the theory but gives a name to an already existing object or function
- theorem: A logical sentence that is a provable consequence of all the axioms of the theory (including implicit axioms, discussed later).
- constructor set: A statement that every object of a certain sort is in the range of at least one of a set of operators. The constructor sets correspond to an implicit structural induction axiom.
A valid sentence is one that is true of all the objects and functions discussed by the specification. Thus the axioms of a specification are valid in the corresponding theory, by definition. The theorems are also valid, because they are provable from the axioms.
For example, in the specification NAT-BASIC in Figure 1, the definition of the predicate nonzero? consists of a single axiom, a logical sentence that asserts that a nonnegative integer is said to be nonzero when it is not equal to zero. Another definition, of the function nat-of-pos, asserts that the constant nat-of-pos stands for the function (relax nonnegative?)--the function relax will be introduced subsequently. Note that sentences are in higher-order logic--the function relax has a predicate nonnegative? as its argument and yields another function; the constant nat-of-pos is equal to that function. Syntax is Lisp-like--thus the successor of x is written (succ x) rather than succ(x) or x.
The specification has axioms, some of them in definitions, and a theorem. Axioms and theorems in specifications are implicitly universally quantified; thus the axiom succ-is-one-to-one holds for all nonnegative integers x and y. In addition to the explicit axioms, which appear literally in the specification, there are implicit axioms corresponding to some specification constructs. The definitions do not alter the theory but merely provide meanings for the defined constants, in this case nonzero? and nat-of-pos. The specification also has axioms that are not definitions, e.g., the axiom succ-is-one-to-one. The theorem is a provable logical consequence of the implicit and explicit axioms. Introducing a theorem does not change the meaning of a specification. (See Sections 1.6 and 1.7 for more on the distinction between axioms, definitions, and theorems.)
The specification has two constructor sets, one for each of its two sorts, Nat and Pos. The first constructor set,
constructors {zero, nat-of-pos} construct Nat
stipulates that every nonnegative integer is either the object zero or is in the range of the function nat-of-pos. The second constructor set
constructors {succ} construct Pos
states that every positive integer is in the range of the successor function succ. Together these constructor sets correspond to an implicit structural induction axiom for the nonnegative integers.
In the subsequent subsections we discuss each of the specification elements in more detail. There are many interdependencies in the discussion. For example, in discussing sorts, we introduce implicit axioms, while the subsequent presentation of axioms relies on our knowledge of the sort structure.
1.1 Sorts
The primitive sorts of a specification are introduced via sort declarations. Each sort declaration consists of the keyword sort or sorts followed by a list of one or more sort identifiers.
An object is never viewed independently of its sort; two objects of distinct sort are never equal. Thus, in the specification NAT-BASIC, 1 viewed as a positive integer is distinguished from 1 viewed as a nonnegative integer; we may imagine that the two versions of 1 are invisibly subscripted, 1Nat and 1Pos. The function nat-of-pos maps each positive integer into the same number viewed as a nonnegative integer; the function succ maps each nonnegative integer into its successor viewed as a positive integer. Thus
(succ 0Nat) = 1Pos
(nat-of-pos 1Pos) = 1Nat
The relationship between the nonnegative integers and the positive integers is illustrated as follows:
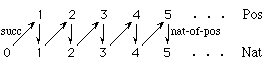
The top row of integers are positive, the bottom, nonnegative. The upward-diagonal arrows indicate the successor function succ, and the downward-vertical arrows indicate the inclusion function nat-of-pos.
Note that the so-called inclusion function is not the identity. It would be a type error to say
(nonzero? (succ x))
because succ yields a positive integer but nonzero? accepts only nonnegative integers. For this reason, the axiom in the specification had to say
(nonzero? (nat-of-pos (succ x)))
We may illustrate the situation by the following figure:
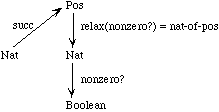
We could have decided to eliminate the sort Pos and declare the successor function to yield a nonnegative integer. That would have simplified this specification but complicated matters later, when we want to extend the specification and define a predecessor function pred to subtract 1 from a positive integer. Using Pos, we can define
op pred : Pos -> Nat
definition of pred is
axiom (equal (pred (succ x)) x)
end-definition
In this theory, the expression (pred zero) has no meaning and is syntactically illegal.
If instead we were to declare
op pred : Nat -> Nat
and revise the axioms accordingly, we would be asserting that (pred zero) is a nonnegative integer, even though the axioms do not determine which nonnegative integer it is. It would thus be a legal operation to take the predecessor of zero. This would be a subtly different version of the theory, not incorrect but different.
As mentioned earlier, the sort Boolean is the sort of the two truth values, true and false. This sort is built into every specification and need not be declared.
1.2 Sort Constructors
Sort constructors are operators that apply to sorts. They are used to generate constructed sorts from primitive sorts or other constructed sorts. Slang has five sort constructors:
- product: Product sorts are denoted by a sequence
E1, E2,...,En of two or more component sorts. They consist of tuples of elements from the component sorts, in order.
- coproduct: Coproduct sorts are denoted by a sequence
E1+E2+...+En of two or more component sorts. Intuitively a coproduct consists of the ``disjoint union'' of elements from the component sorts.
- function: A function sort is denoted by
D -> E, where D is a domain sort and E is a range (or codomain) sort. It consists of functions from the domain sort D into the range sort E.
- quotient: Quotient sorts are denoted by
E/r?, where E is a base sort and r? is an equivalence relation. It consists of the equivalence classes of elements of the base sort E modulo the equivalence relation r?.
- subsort:
Subsorts are denoted by a E|p?, where E is a supersort and p? is a unary predicate. It consists of those elements of the supersort E that satisfy the predicate p?.
A sort term is either the name of a primitive sort or a term obtained by applying a sort constructor to other sort terms. We shall now describe each of the sort constructors in a little more detail.
1.2.1 Product Sorts
If e1 through en are of sorts E1 through En, respectively, then
<e1 e2 ... en>
is a tuple whose sort is the product E1,E2,...,En. For example, if one is of sort Nat and X is of sort Atom, then <one X> is of sort Nat, Atom.
In Specware, an operation that we think takes multiple arguments actually takes only a single argument, a tuple. For example, the binary relation br is declared as follows:
op br : E, E -> Boolean
The term ``E, E'' is a product sort; it indicates that the predicate br takes a tuple of two arguments, both of sort E. In practice, we are more likely to write (br e1 e2) than (br <e1 e2>), but both are legal and they have the same meaning.
The empty product sort () contains a single tuple, the empty tuple <>. When the empty product occurs as the domain of a function sort, its syntax may be omitted. Thus, instead of writing () -> F, we may write -> F.
There are two kinds of built-in operations on every product sort: an n-ary tuple constructor, which constructs elements of the product sort, and n projection functions, which select components of tuples. The constructor function maps elements e1,...,en into the tuple <e1 ... en>. Each projection function (project i) is of sort
(project i): E1,...,En -> Ei
It maps <e1 ... en> into ei. The application of a projection function is written as ((project i) <e1 ... en>).
Note that project is a higher-order function; it maps i into (project i). Also, project is polymorphic; hence, it is implicitly indexed by the product sort, as in (projectE1,...,Eni). Thus (projectA1,A21) is distinct from (projectB1,B21) even though both would be written (project 1); the ambiguity is resolved by type inference. Tuples can be nested--thus <a <b c>> is a legitimate tuple.
For each product sort, there corresponds a set of implicit axioms (See ``Axioms and Theorems,'' Section 1.6) that serve as the definition of the projection functions. These axioms do not appear literally in the specification, but will be used automatically in proving theorems in the corresponding theory. For a product of two sorts, ``E1, E2'', we have two implicit axioms:
(equal ((project 1) <e1 e2>) e1)
(equal ((project 2) <e1 e2>) e2)
Similarly, for a product of n sorts we have n analogous implicit axioms.
Two tuples are equal only if their respective components are all equal. Thus, if <d1 d2> equals <e1 e2>, we know that d1 equals e1 and d2 equals e2.
1.2.2 Coproduct Sorts
The coproduct of a set of sorts may be thought of as their disjoint union. In other words, each element of any of the component sorts corresponds to an element of the coproduct, and no two elements of distinct components correspond to the same element of the coproduct. The structure is known as a variant record in some programming languages.
For example, if E1 is a sort containing two elements X and Y, and E2 is a sort containing two elements Y and Z, then E1+E2 is a sort containing four elements X, Y, Y, and Z. We may imagine that the two elements originating in sort E1 have invisible subscripts 1, and the two elements originating in E2 have invisible subscripts 2; at any rate, the two copies of Y are not equal. The situation is illustrated by the following figure:
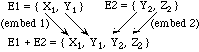
The empty coproduct, [], is the coproduct of zero components; it has no elements.
For every coproduct sort, there is a family of embedding operations, one for each component sort. The embeddings map elements of the component sorts into the coproduct sort. For each i = 1, ... ,n, we have
(embed i): Ei -> E1+...+En
Thus, in the above example, (embed 1) maps E1 into E1+E2. The element X1 of E1 maps into X1 of E1+E2 and Y1 of E1 maps into Y1 of E1+E2.
The function embed is higher order and polymorphic (similar to project). Thus an application is written ((embed i) ei), with the embed symbol implicitly indexed
(embedE1+...+Eni)
The embedding function is defined by the following axioms, which are present implicitly in the specification in which the coproduct appears. For a coproduct of two sorts, E1+E2, we have
(implies (equal ((embed 1) d1) ((embed 1) e1))
(equal d1 e1))
(implies (equal ((embed 2) d2) ((embed 2) e2))
(equal d2 e2))
That is, embeddings are one-to-one (injective); two distinct elements in a component cannot map into the same element in the coproduct.
(fa (d : E1+E2)
(or (ex (e1 : E1) (equal d e1))
(ex (e2 : E2) (equal d e2))))
That is, embeddings are collectively surjective; every element in the coproduct is mapped onto by some element in one component.
(not (equal ((embed 1) e1)((embed 2) e2)))
That is, embeddings have disjoint images; elements from distinct components cannot map onto the same element in the coproduct.
Analogous implicit axioms hold for coproducts of more than two sorts.
1.2.3 Function Sorts
Given a domain sort D and a range (or codomain) sort E, the function sort D -> E contains the functions from D into E. Most operations belong to function sorts. For example, the reflexive-closure operation cl maps one binary relation into another:
op cl : (E,E -> Boolean) -> (E,E -> Boolean)
There are two built-in operations on function sorts, the lambda term constructor and the application operation.
If D is a sort term and exp is a term of sort E, then the lambda term
(lambda (d : D) exp)
is of sort D -> E. Occurrences of d in exp must be of sort D; if the sort of d can be determined to be of sort D syntactically, we may omit the sort term, as in
(lambda (d) exp)
The resulting lambda term stands for the function that, for input d, yields the value of the corresponding term exp. The variable d is regarded as a bound variable of the lambda term. Similarly for sequences of variables (x1 x2 ... xn); thus
(lambda (x1 x2) (plus (times x1 x1) x2))
is of sort Nat, Nat -> Nat in a specification in which plus and times also have that sort.
If f is a function of sort D -> E and d is a term of sort D, then the apply operation yields the result (f d) of applying f to d. (See Section 1.5.)
The operations on functions satisfy two implicit axioms: an alpha rule that allows us to rename bound variables systematically without changing the value of a term, and a beta-rule for application, namely (in the one-variable case)
(equal ((lambda (d) ex p) arg)
exp[arg])
Here exp[arg] is the result of replacing all occurrences of d in exp with arg, renaming bound variables systematically if necessary to avoid name clashes.
1.2.4 Quotient Sorts
Given a base sort E and an equivalence relation
r?: E, E -> Boolean
the sort E/r? denotes the quotient sort of E modulo r?. The elements of the quotient sort E/r? are equivalence classes of elements of the base sort E. For each quotient sort E/r?, there is a built-in abstraction function which maps each element of the base sort to the equivalence class that contains it. This abstraction function, called quotient, is a higher-order polymorphic function:
(quotient r?) : E -> E/r?
For example, suppose Sixteen is a sort consisting of the integers from 0 through 15; we arrange them in a rectangular arrays follows:
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15
Let mod4? be the relation that holds between two elements of Sixteen if they both belong in the same column of the above array; thus (mod4? 1 9) is true but (mod4? 5 6) is not.
Then Sixteen/mod4? is the sort of equivalence classes of elements, where two elements are in the same class if the relation mod4? holds between them; in other words, Sixteen/mod4? is the sort of columns in the above array. The abstraction function (quotient mod4?) maps a nonnegative integer in Sixteen into the column in which it appears. Thus ((quotient mod4?) 2) and ((quotient mod4?) 6) are both equal to the third column of the array.
The abstraction function quotient is defined by the following implicit axioms:
(iff (r? e1 e2)
(equal ((quotient r?) e1)
((quotient r?) e2)))
That is, the equivalence relation r? on E maps under abstraction into the equality relation on E/r?. For example, two elements in the Sixteen array are equivalent with respect to the relation mod4 if and only if the columns they appear in are equal. Also
(fa (d : E/r?)(ex e : E) (equal d ((quotient r?) e)))
In other words, the abstraction function is surjective. For example, every column in the Sixteen array contains an element.
1.2.5 Subsorts
Given a sort E and a unary predicate p?: E -> Boolean, the sort E|p? denotes the subsort of E generated by p?. The subsort E|p? consists of those elements of the supersort E that satisfy the predicate p?. For each subsort E|p?, there is a built-in inclusion function, which maps elements of the subsort to the corresponding elements of the supersort. This inclusion function is called relax, and is a higher-order polymorphic function:
(relax p?) : E|p? -> E
For example, in the specification NAT-BASIC for the nonnegative integers on page 4, the positive numbers have been defined to be the subsort of those nonnegative integers that satisfy the predicate nonzero?. The function nat-as-pos was defined to be equal to the inclusion function (relax nonzero?), the function that maps each positive integer x into the nonnegative integer x.
One might think that (relax p?) is the identity function, since it maps an element into itself. But, as we have noted earlier, it maps x viewed at an element of the subsort into x viewed as an element of the supersort; these are not the same because we don't think of the element as existing independently of its sort.
Another example: in the specification for arrays, (see Appendix E on page 160) an array a may have entries a[0], ... , a[n-1], where n is the size of the array. To represent this in the specification, we introduce a function access-array, which is intended to return the value of the array entry a[i] for given array a and index i.
Suppose E is the sort of the entries. If we declared our function with the signature
op access-array : Array, Nat -> E
it would mean that our access function would have to return an array entry a[i] for every nonnegative integer i, even though the array only has entries when i is less than the size of a. So instead we declare our function with the signature
op access-array : ((Array, Nat) | in-bounds?) -> E
Here in-bounds? is a predicate that holds only for an array a and index i such that i is less than the size of a. Thus the function access-array is only defined on a subsort of the product of arrays and nonnegative integers, those for which the integer is within the bounds of the array.
In that specification, applying the function (relax in-bounds?) to an element, say ai, of the subsort, yields a corresponding pair <a,i>. One must be careful to apply the function access-array only to the subsort element ai, not to the pair <a,i>.
The definition of the inclusion function relax is provided by the following implicit axioms:
(p? ((relax p?) d))
(implies (p? e)
(ex (d : E|p?) (equal e ((relax p?) d))))
In other words, the subsort consists of those elements of the supersort that satisfy the predicate. For example, every positive integer corresponds to a nonnegative integer that satisfies the relation nonzero?, and vice versa. Also
(implies (equal ((relax p?) d1) ((relax p?) d2))
(equal d1 d2))
That is, the inclusion function is injective (one-to-one). For example, it is impossible for two distinct positive integers to correspond to the same nonnegative integer.
1.2.6 Precedence
The product and coproduct sort constructors ``,'' and ``+'' have equal precedence, which is higher than that of the function sort constructor ``->''; thus ``C, D -> E'' is parsed as the function sort ``(C, D) -> E,'' not as the product sort ``C, (D -> E).''
Similarly, the subsort and quotient sort constructors ``|'' and ``/'' have equal precedence, which is higher than that of the product or coproduct, ``,'' or ``+''; thus ``D + E|p?'' is parsed as ``D + (E|p?).'' This precedence may be overridden by using parentheses.
The function sort constructor ``->'' is right associative; thus ``C -> D -> E'' is parsed as ``C -> (D -> E).'' The product and coproduct sort constructors are not associative; insertion of parentheses corresponds to grouping, and will generate different products and coproducts from the ungrouped version.
1.3 Sort Axioms
Sort axioms can be used to assert an equivalence between an (elsewhere introduced) primitive sort and a constructed sort. The sorts and operations used in a sort axiom must be declared separately. The left side of a sort axiom must be a primitive sort; the right side can be either a primitive sort or a constructed sort.
For example, the specification NAT-BASIC contains the sort axiom
sort-axiom Pos = Nat | nonzero?
where the sorts Pos and Nat and the operation nonzero? have already been declared. (In this case there is actually a definition for nonzero?, but this is not required for the predicate to be mentioned in a sort axiom).
There is a semantic freeness restriction: sort axioms cannot be used to assert the equivalence between constructed sorts that are not structurally equivalent. For example, a sequence of sort axioms
sort-axiom A = B, C sort-axiom A = B -> C
in a specification will result in an error message--A cannot be both a product and a function sort. This is an implementation decision to simplify the type-checking--it may change in future versions.
1.4 Operations
Specifications introduce operations as named constants of a specified sort. For example, NAT-BASIC contains the following operation declarations:
const zero : Nat
op nonzero? : Nat -> Boolean
Each operation declaration consists of the keyword op or const followed by the name of the operation, followed by a colon and a sort term which specifies the signature of the operation. Typically, the signature of an op is a function sort and the signature of a const is a primitive sort, but they may be used interchangeably and the signature can be any sort term. The system chooses a specific keyword while printing: op if the signature of the operation is a function sort, and const otherwise.
It is permissible in a specification to give two distinct sort declarations to the same operation symbol. However, these will be treated as declarations for two distinct operations with the same name. If in subsequent expressions the type-checker cannot determine which operation is being referred to, it is regarded as an error. For example, every sort has a corresponding equality relation--different operations with the same name.
Constants vs. Nullary Operations. Note that the two declarations
op f : E
op f : -> E
introduce two different operations; the former denotes a constant while the latter denotes a 0-ary function. A constant is not identical to a 0-ary function; the difference between them becomes apparent when they are used in a term (see Section 1.5); the former appears as f while the latter appears as (f).
1.4.1 Built-in Operations
Built-in operations are declared implicitly in a specification and need not be declared explicitly. We have mentioned built-in operations associated with certain sort terms, such as relax, quotient, lambda, project, and embed. There are also built-in boolean operations: the constants true and false, the unary not, and the binary and, or, implies, and iff; all yield a boolean. Note that there is no n-ary and or.
1.4.2 Quantifiers
The boolean universal quantifier fa and existential quantifier ex are built-in boolean operations. If D is a sort term and exp is a term of sort boolean, so are the quantified terms
(fa (d : D) exp)
which means that exp holds for all d of sort D, and
(ex (d : D) exp)
which means that exp holds for some d of sort D. The symbol d is regarded as a bound variable in the quantified term. As in the case of lambda terms, the occurrences of d in exp must be of sort D, and the sort term may be omitted if it is redundant. If an undeclared operator appears in an axiom or theorem, it will be given implicit universal quantification (see Section 1.5).
For example, in the specification NAT-BASIC, we have the theorem
(fa (x : Pos) (ex (y : Nat) (equal x (succ y))))
Because the domain of succ is Nat, we can determine syntactically that the sort of y is Nat and omit that sort declaration. Similarly, because the range of succ is Pos we can determine the sort of x syntactically and omit that sort declaration. Finally, we can omit the universal quantification on x, because it is there implicitly. Thus the above theorem could have been written as follows with no change of meaning:
(ex (y) (equal x (succ y)))
The former way of writing the theorem is less surprising, however.
The sort term D may be primitive or constructed. For example, we have seen the implicit axiom for the abstraction function
(fa (d : E/r?)(ex e : E) (equal d ((quotient r?) e)))
1.4.3 Equality
For every sort, there is a built-in equality relation equal declared implicitly on that sort. These relations are all represented by the same symbol--type inference must resolve any ambiguity. The built-in boolean operator iff is identified with the equality relation on the sort Boolean; the two may be used interchangeably on boolean terms. If two objects within a sort are equal, the results of applying any operation to them will also be equal--they are indistinguishable within that specification.
The equality relation satisfies the following implicit axioms:
(equal x x)
For given sorts D and E and operation f : D -> E,
(implies (equal d1 d2)
(equal (f d1) (f d2)))
It is not necessary to declare the equality relation for a sort, and it is illegal to provide a definition: the relation is already defined. If a relation equal for a sort is declared explicitly in a specification, it will be treated as distinct from the built-in equality relation for that sort. It is permissible, however, to provide axioms that constrain the meaning of the equality relation. For example, in the specification NAT-BASIC on page 4, the axiom succ-is-one-to-one asserts that the equality relation cannot hold between the successors of two distinct nonnegative integers.
1.5 Terms and Formulas
Terms are constructed according to conventional rules of typed lambda calculus. In particular:
- Each constant is a term.
- If
d is a term of sort D and f is an operator of sort D -> E, then the application (f d) is a term of sort E.
We have introduced the term-construction rules for the other built-in operators in the appropriate sections. A formula is a term of sort boolean.
All functions in Slang accept one argument and return one result. Functions that accept more than one argument , or none , and functions that return more than one value are handled by accepting and returning tuples. The function application notation implicitly builds tuples if there is more than one argument. For example, (plus x y) is parsed as (plus <x y>).
When there is only one argument, a tuple is not automatically constructed. As a consequence, the composition (union (split s)) below is well-formed:
op union : Set, Set -> Set
op split : Set -> Set, Set
axiom (equal s (union (split s)))
The appendix (Appendix C) contains a table of terms in Slang and their sorts.
1.6 Axioms and Theorems
Axioms and theorems in a specification are formulas that use the symbols (sorts and operations) appearing in the signature of that specification. The distinction between axioms and theorems is that theorems can be proved from the rest of the specification and thus do not add to the theory generated by the specification. The order of the axioms and theorems in a specification is not significant.
For example, the specification NAT-BASIC contains the axioms
axiom (iff (nonzero? x) (not (equal x zero)))
axiom (equal nat-of-pos (relax nonzero?))
axiom (nonzero? (nat-of-pos (succ x)))
axiom succ-is-one-to-one is
(implies (equal (succ x)(succ y)) (equal x y))
and the theorem
theorem (fa (x : Pos) (ex (y : Nat) (equal x (succ y))))
Note that the name of an axiom or theorem is optional.
As we have remarked, if an undeclared operator appears in an axiom or theorem, it will be given implicit universal quantification. For example, suppose a specification contains an axiom (p e), where neither p nor e has been declared. Then the axiom will be taken as an abbreviation for
(fa (p e) (p e))
In other words, every predicate holds for every argument. The system will give a warning that p is not declared, because p is syntactically in the position of an operator--it is probably an error. It will give no warning about e because e is in the position of an argument--it assumes that e is intended to be universally quantified. The omitted initial universal quantifiers will be added internally; however, the system will print the formula in the original form, without the quantifier prefix.
Type inference is used to deduce the types of omitted quantifiers. For example, as we have remarked, the theorem
theorem (fa (x : POS) (ex (y : NAT) (equal x (succ y))))
may also be written
theorem (ex (y) (equal x (succ y))
In addition to the explicit axioms, which appear literally in the specification, we have seen that there are implicit axioms corresponding to the equality relation, the sort constructors, the constructor sets, and other operations that are built into specifications.
Each specification corresponds to a theory and defines a class of ``models'' of the theory. Informally, a model of a specification may be regarded as a structure, i.e., a collection of sets and functions, that it applies to. The axioms, explicit and implicit, determine the class of models; each axiom, unless it is redundant, outlaws some models. For example, without the axiom succ-is-one-to-one, the specification NAT-BASIC on page 4 would have additional models, in which the successor of 8 would be the same as, say, the successor of 4, namely 5; these models are excluded by the axiom.
The theorems of a specification, on the other hand, do not alter the class of models--they apply to any model that satisfies the axioms of the specification. In principle, the theorems could be proved by the automatic theorem prover to follow from the axioms, although this is not currently enforced by the system.
Consistency. It is quite possible to write specifications that contain inconsistent sets of axioms, and it is impossible in general to check specifications for consistency. (The consistency of common specifications for set theory have been questioned by mathematicians.) If a specification is inconsistent, any sentence in its language is a theorem, so it cannot be relied on for establishing correctness.
On the bright side, the specifications in Specware for implementation languages, such as Lisp, have been subjected to a good deal of scrutiny and are believed to be correct and hence consistent. If we succeed in finding a refinement of a source specification into a consistent target specification (see Section 3), the consistency of the source specification is established. Thus, by using Specware to implement a specification, we construct a proof of its consistency, relative to that of the implementation theory.
1.7 Definitions
A definition for an operation f:D -> E in Slang is a set of axioms that characterize f. For example, the specification NAT-BASIC defines the predicate nonzero? as follows:
definition of nonzero? is
axiom (iff (nonzero? x) (not (equal x zero)))
Larger specifications for the nonnegative integers also contain definitions for plus, which adds two nonnegative integers, and pred, which subtracts 1 from a positive integers:
definition of plus is
axiom (equal (plus zero y) y)
axiom (equal (plus (nat-of-pos (succ x)) y)
(nat-of-pos (succ (plus x y))))
end-definition
definition pred-def of pred is
axiom (equal (pred (succ x)) x)
end-definition
Syntactically, a definition is a set of axioms enclosed by the pair of keywords definition and end-definition. Optionally, the definition may have a name or the name of the operation being defined, or both. Note that the user may select the name of the definition but the name of the operation in the heading must agree with the actual name of the operation that appears in the axioms. See the BNF grammar in the Appendix (B.1) for the precise syntax of definitions
A definition does not change the class of models for the specification, but it does assign a name to an object or function that exists in each of the models. For example, in each model for the nonnegative integers, there exists a unique function that maps x +1 into x; the effect of the definition pred-def is to declare that the name of that function is pred, not to eliminate any of the models.
1.8 Constructor Sets
A constructor set is a set of operations with the same range sort; it implicitly introduces an induction axiom for that sort. It means that every element of the range sort can be obtained by repeated application of the elements of the constructor set.
Suppose a specification for binary trees contains a constructor set
constructors {at, cons} construct Tree
where the specification contains the following operator definitions:
at: Atom -> Tree cons: Tree, Tree -> Tree
In other words, each atom a corresponds to a binary tree (at a), and any two trees s and t can be combined into a new tree (cons s t).
Here are some binary trees; X and Y are atoms:
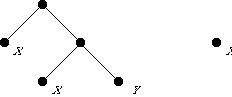
The right tree is the image, under at, of the atom X. The left tree is the result of applying the function cons to two other trees.
The intended meaning of the constructor set is that every tree either corresponds to an atom or can be obtained by repeatedly combining other binary trees.
From this constructor statement, the following induction axiom will be introduced implicitly:
(fa (p)
(implies
(and
(fa (a : Atom) (p (at a)))
(fa (s : Tree t : Tree)
(implies (and (p s) (p t)) (p (cons s t)))))
(fa (t : Tree) (p t))))
In other words, to prove that a property is true of all trees, it suffices to show two conditions:
Not Disjoint. Note that constructor set declaration does not imply that the images of the constructors are disjoint. Sometimes this property can be asserted by explicit axioms, e.g.,
axiom (nonzero? (nat-of-pos (succ x)))
asserts that the images of nat-of-pos are distinct from zero.
2 Morphisms and Diagrams
2.1 Overview of Specification-Constructing Operations
There are four ways of constructing a specification in Slang:
- basic--form a basic specification as a set of specification elements (sorts, sort axioms, operations, axioms/theorems, definitions, and constructor sets).
- translate--copy a specification while renaming some symbols (see Section 3.1).
- import--enrich an imported specification with additional specification elements (see Section 2.3).
- colimit--take the colimit of a diagram of specifications (see Section 3.4)--this is the primary means for combining two or more specifications.
The basic form explicitly constructs a specification, while the next three are specification-constructing operations which take as arguments specifications and diagrams, and yield specifications. The four ways of constructing specifications should be considered as expressions that yield specifications. Wherever a specification is expected in these or other expressions, the name of a specification can be substituted.
The operations translate, import, and colimit will be described in Section 3. However, before these operations can be explained, morphisms and diagrams need to be described. In particular, before applying the colimit operations, which combines more than one specification, we must indicate how the specifications are to relate with each other. The way of relating specifications in Specware is in terms of a morphism that describes how one specification can be viewed as part of another. The colimit is applied to a diagram of specifications related by morphisms. Furthermore, each of the operations constructs new morphisms that describe how the newly constructed specification is related to the given ones.
2.2 Morphisms
Definition 2.1: Morphism. A morphism is a mapping from a specification called the source specification to a specification called the target specification. Intuitively, it describes how the source theory can be regarded as a part of the target theory. A morphism m from a source specification S to a target specification T maps the sorts of S into the sorts of T, and the operations of S into the operations of T such that
We shall write m : S ->T to indicate that the morphism m has source S and target T, i.e., m maps S intoT.
When an element of S is mapped into an element of T under a morphism, that means those elements are being identified. For example, a morphism that maps the sort Seq into the sort Array is identifying the sequences with the arrays, in the appropriate specifications.
Morphisms are described in Slang by listing a translation of each of the explicitly declared sorts and operations. The translation of constructed sorts and formulas is then computed inductively. Morphisms are represented by expressions of the form
morphism [name] : <source spec> -> <target spec> is
{<name> -> <name>,
<name> -> <name>,
...}
Every symbol of the source specification must be mapped into a symbol of the target specification; however, if a symbol of the source specification is not mentioned explicitly in the mapping, it is assumed that it is mapped into a symbol of the same name in the target specification.
Although we have said that the source theory can be regarded as part of the target theory, in fact multiple elements of the source theory can be mapped into the same element in the target theory. That is, distinct sorts can map into the same sort, or distinct operations can map into the same operation.
We typically give only the name of the source and target specifications in a morphism, and define the corresponding specifications elsewhere, but we may provide any expression whose value is a specification. The name we give to a morphism is optional. The precise syntax for a morphism is given in the appendix (Section B.1, Syntax).
Let us define the identity morphism and the composition operation for morphisms.
Definition 2.2: Identity and Composition. For any specification S, the identity morphism is the morphism whose source and target are both S and which maps each element of S into itself.
For any morphisms m : R ->S and n : S ->T, the composition of m and n is a morphism m; n : R ->T, which maps each element of S into the result of applying first m and then n.
The reader should be convinced that the identity morphism and the composition of two morphisms are indeed morphisms.
We begin with a toy example and continue with a more meaningful one.
Example 2.3 Consider the following two specifications:
spec FOO is spec BAR
sort A, B sort C, D, E
op f: A -> B op g: C -> D
end-spec op h: D -> E
end-spec
The following morphism MOO is well-formed.
morphism MOO : FOO -> BAR is
{A -> C,
B -> D,
f -> g}
It might be illustrated like this:
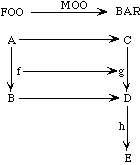
Here the function f is mapped into the function g; hence the domain A of f is mapped into the domain C of g, and the range B of f is mapped into the range D of g.
A second mapping GOO is not a well-formed morphism:
morphism GOO : FOO -> BAR is
{A -> C,
B -> E,
f -> g}
It might be pictured like this:
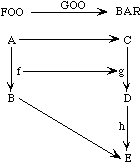
Here the function f is mapped into the function g, but the range B of f is not mapped into the range of g.
We follow with a more substantive example.
Example 2.4 Morphism over Pairs.
As an example, suppose we have the two specifications for pairs of elements. In the first specification, PAIR (Figure 2) each component of a pair is of a different sort, D and E respectively. For example, if D is the letters of the alphabet and E is the decimal digits, [X, 2] would be of sort Pair.
spec PAIR is
sorts D, E, Pair
op make-pair : D, E -> Pair
op first : Pair -> D
op second : Pair -> E
axiom (equal (first (make-pair d e)) d)
axiom (equal (second (make-pair d e)) e)
constructors {make-pair} construct Pair
theorem (equal p (make-pair (first p) (second p)))
end-spec
Figure 2: The Specification PAIR
The function make-pair forms a pair from two elements, of sorts D and E respectively. Thus makepair applied to X and 2 yields the pair [X, 2]. There are two functions, first and second, that extract the first and second components, respectively, from a pair. Thus first and second applied to [X, 2] yield X and 2, respectively.
The axioms and theorem describe the relationships among these functions. The constructor statement, in this case, corresponds to an implicit axiom
(fa (P)
(implies
(fa (d : D e : E) (P (make-pair d e)))
(fa (p : Pair) (P p))))
In other words, to show that a property holds for all pairs, it suffices to show that it holds for all pairs of form (make-pair d e). (It follows that all pairs actually have this form.) This is a degenerate induction axiom; it has no induction hypothesis, because the function make-pair in the constructor set does not take an argument of sort Pair; its arguments are of sorts D and E, but these sorts have no constructor set. The induction axiom for binary trees (Section 1.8), in contrast, is a proper induction axiom, because the function cons in the constructor set for the sort Tree takes arguments of sort Tree.
spec CONS-PAIR is
sorts Atom, Pair
op cons : Atom, Atom -> Pair
axiom uniqueness is
(implies (equal (cons a b) (cons aa bb))
(and (equal a aa) (equal b bb)))
constructors {cons} construct Pair
op head : Pair -> Atom
op tail : Pair -> Atom
definition of head is
axiom (equal (head (cons a b)) a)
end-definition
definition of tail is
axiom (equal (tail (cons a b)) b)
end-definition
theorem (equal p (cons (head p) (tail p))
op rev-pair : Pair -> Pair
definition of rev-pair is
axiom (equal (rev-pair (cons a b)) (cons b a))
end-definition
end-spec
Figure 3: The Specification CONS-PAIR
In the second specification, CONS-PAIR (Figure 3), both components of a pair are of the same sort, Atom. For example, if Atom is the letters of the alphabet, [X, Y] would be of sort Pair.
The functions cons, head, and tail play the role of make-pair, first, and second, respectively, in PAIR. In addition, CONS-PAIR includes the definition of a function rev-pair that reverses the components of a pair; thus the result of reversing the pair [X, Y] is [Y, X]. We could not define this function in the first specification, PAIR, because the result of reversing a pair would not be a pair--the sorts would be reversed. The following morphism, then, embeds PAIR into CONS-PAIR and indicates the relationship between these two specifications:
morphism PAIR-TO-CONS-PAIR : PAIR -> CONS-PAIR is
{D -> Atom,
E -> Atom,
make-pair -> cons,
first -> head,
second -> tail}
Note that the mapping associates each primitive sort or operation symbol in the source specification with a corresponding primitive sort or operation symbol, respectively, in the target specification. The sort symbol Pair from the specification PAIR is mapped into the same symbol in the specification CONS-PAIR, even though no replacement Pair -> Pair is included explicitly in the mapping.
Definitions vs. Axioms. Note that in the specification PAIR, the axioms for first and second are not regarded as definitions, because they restrict the models of the specification. Without these axioms, for example, we could have a model in which there were many elements of sort D or E but only one pair, p1; in such a model, whatever its arguments, the value of (make-pair d e) would be p1.
The axioms for first and second preclude this possibility. If there are at least two distinct elements of sort D, say d1 and d2, the axiom for first would then imply that the first element of p1 =(make-pair d1 e) is d1, and also that the first element of p1 = (make-pair d2 e) is d2, which is impossible. Similarly, if there are at least two distinct elements of sort E, the axiom for second implies a contradiction.
On the other hand, the definitions for head and tail in the specification CONS-PAIR are true definitions. The uniqueness axiom of this specification already guarantees that there cannot be any such bizarre models. From this axiom and the implicit axiom corresponding to the constructor set, we can establish that there exist unique functions satisfying the axioms for head and tail; the definitions serve only to name these functions.
In this case, each axiom of the source specification is mapped into an axiom of the target specification. Thus, the axiom for first from the specification PAIR:
axiom (equal (first (make-pair d e)) d)
is mapped into the definition of head in the specification CONS-PAIR:
axiom (equal (head (cons a b)) a)
(Here a, b, d, and e are dummy variables: they are implicitly quantified universally and do not need to be translated.) In general, however, it would suffice if each axiom from the source were mapped into a theorem of the target; the theorem need not be listed explicitly in the target specification, so long as it is provable from the axioms of the target.
Observe that we could not define a morphism between CONS-PAIRS and PAIR, because we cannot map the sort Atom into two distinct sorts D and E.
Morphisms and Built-In Constructs. The translations for built-in sorts and operations cannot be specified in a morphism. These entities are automatically translated to the corresponding built-in entities in the target. Examples of built-in entities are the sort Boolean, the Boolean operations (and, or, not, etc.), quantifiers (fa, ex, lambda, etc.), and equality.
Note that if the morphism m maps the sort S into the sort T, then m maps the built-in equality on S into the built-in equality on T. You cannot use a morphism to map the equality relation on the source sort into another relation r on the target sort; the built-in axioms for equality on S would map into sentences that must hold for r on T, and equality is the only relation on a sort that satisfies these equality axioms.
Morphisms and Constructed Sorts. Morphisms are defined as symbol maps of the basic sorts and are extended to maps on sort expressions in the natural way. This means that since the morphism MOO mentioned earlier maps sorts A into C and B into D, it also maps, for example, the constructed sort A, B -> A into C, D -> C.
Local Morphisms. In contexts where a morphism needs to be mentioned and the source and the target of the morphism can be inferred, it is only necessary to specify the rules which make up the morphism; the source and target may be omitted. This will be illustrated subsequently, e.g., in Example 2.5.
The source and target of a morphism are sometimes referred to as its domain and codomain. The image of a morphism comprises those elements of its codomain that are mapped onto by some elements of its domain; thus E is in the image of {X -> E} but D is not. We say that a morphism is injective or one-to-one if it doesn't collapse two distinct sorts or operations of its domain into a single sort or operation, respectively, of its codomain; thus {X -> E, Y -> E} is not one-to-one.
Morphism Terms. In some contexts an entire morphism can be identified by a keyword; the domain (source), codomain (target), and rules can then be determined by context. For instance, associated with every specification is the identity morphism, which maps every sort and operation onto itself. If the domain is determined by the context, this morphism can be denoted by the keyword identity-morphism. There is no syntax in Slang for denoting the composition of two morphisms; this is done using the graphical facilities of Specware.
The specification-building operations, which are introduced briefly in Section 2.1 and are fully described in Section 3, not only construct specifications but also construct one or more morphisms which relate the constructed specifications and their components. See the relevant subsections of Section 3 for more on the morphisms constructed by the specification-building operations translate, import, and colimit. These morphisms can be referred to using appropriate keywords, provided the context determines the source, target, and rules.
2.3 Diagrams
A diagram is a directed multigraph whose nodes are labeled with specifications and whose arcs are labeled with morphisms. A multigraph differs from a graph in that there may be more than one arc between nodes. For a diagram to be well formed, the source and target specifications of each of the morphisms must be the same as the specifications that label the source and target nodes of the corresponding arc. To give an example of a diagram, let us first introduce some simple specifications.
Example 2.5 Preorder Diagram.
Here is a basic specification for the theory of reflexive relations:
spec REFLEXIVE-RELATION is
sort E
op rr : E, E -> Boolean
axiom reflexive is (rr e e)
end-spec
In this specification, the operation rr stands for a reflexive relation, such as <= or iff; thus if rr stands for <=, the condition (rr d e) would mean d <=e. The reflexive axiom states the reflexive property of the relation.
Here is a specification for the transitive relations:
spec TRANSITIVE-RELATION is
sort E
op tr : E, E -> Boolean
axiom transitive is
(implies (and (tr c d) (tr d e))
(tr c e))
end-spec
The operation tr in this specification plays the role of rr in the specification for the reflexive relations. The transitivity axiom states the transitivity property of the relation tr.
In introducing the colimit construction in Section 3.4, we will want to combine these two specifications to yield the notion of a preorder, which satisfies the axioms of both specifications. For this purpose we must indicate which components of these specifications are to be identified. We therefore introduce a third specification, which describes what these two specifications have in common. This is the basic specification for a binary (two-argument) relation:
spec BINARY-RELATION is
sort E
op br : E, E -> Boolean
end-spec
The specification is analogous to the preceding two, but it has no axioms.
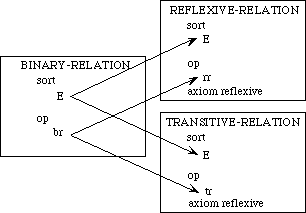
Figure 4: Diagram for a Preorder
To combine these specifications we must indicate with a diagram what elements are to be identified. In graphical form, such a diagram is illustrated in Figure 4. The diagram indicates that the operation rr in the reflexive-relation specification is to be identified with the operation tr in the transitive-relation specification. The binary-relation specification acts as an intermediary in making these identifications. Morphisms map constructs from the binary-relation specification into the corresponding constructs in the other two specifications; if one construct is mapped into the other, the two are to be identified.
The morphism that links the specification for binary relations to the specification for reflexive relations is
morphism BIN-REL-TO-REFLEXIVE :
BINARY-RELATION -> REFLEXIVE-RELATION is
{br -> rr}
It indicates that the operation br is to be identified with the operation rr.
The morphism that links the binary-relation specification to the transitive-relation specification is
morphism BIN-REL-TO-TRANSITIVE :
BINARY-RELATION -> TRANSITIVE-RELATION is
{E -> E,
br -> tr}
The rule E -> E could have been omitted, since both sorts have the same name E. Note that this morphism maps the operation br into the operation tr.
In the diagram of Figure 4, the nodes are the three specifications and the arcs are the two morphisms. This diagram is represented textually as follows:
diagram PREORDER-DIAGRAM is
nodes BINARY-RELATION, REFLEXIVE-RELATION, TRANSITIVE-RELATION
arcs BINARY-RELATION -> REFLEXIVE-RELATION : BIN-REL-TO-REFLEXIVE,
BINARY-RELATION -> TRANSITIVE-RELATION : BIN-REL-TO-TRANSITIVE
end-diagram
When the colimit operation is applied to this diagram, the three theories will be combined and the constructs that are linked by morphisms will be identified. For instance, since br is mapped into rr by one morphism and into tr by the other, all three operations will be identified in the colimit specification. This will be discussed further in Section 3.4.
We could not have constructed a morphism directly between REFLEXIVE-RELATION and TRANSITIVE-RELATION, or vice versa, because each specification has an axiom that would not be mapped into a theorem of the other. But we were able to construct morphisms from the impoverished specification BINARY-RELATION into the other two.
Note that, as we mentioned in Section 2.2, we are able to specify the morphism by merely listing the rules; we may omit the names BINARY-RELATION and REFLEXIVE-RELATION of the source and target specifications, respectively, because these are the same as the labels of the nodes at the ends of the arc, and can be inferred.
In our example of a diagram, we have given specification names as the nodes. As usual, it is permissible to give instead any expression whose value is an unnamed specification; similarly, we may give sets of rewriting rules or morphism terms instead of morphism names. Thus, the first arc of the preorder diagram could have been written
spec
sort E
op br : E, E -> Boolean
end-spec
-> REFLEXIVE-RELATION : {br -> rr}
3 Specification-Building Operations
Now that we have discussed morphisms and diagrams, we can introduce the operations for constructing a specification from other specifications: translate, import, and colimit.
3.1 Translate
The translate operation creates a copy of a specification, perhaps renaming some components. Here is an example:
Example 3.1 Translated Binary Relations.
The specification BINARY-RELATION was introduced on page 35. The expression
translate BINARY-RELATION by
{br -> rr}
rewrites the specification according to the indicated replacements. The resulting specification is as follows:
spec TRANSLATED-BINARY-RELATION is
sorts E
op rr : E, E -> Boolean
end-spec
Note that the first expression translate ... cannot be given at the top level because it is not named; it could not be referred to elsewhere.
Translation is often used to introduce a more convenient or conventional vocabulary into a specification. The translation in the example will be useful when we want to reconstruct the specification REFLEXIVE-RELATION by importing the specification BINARY-RELATION (see Section 2.3, instead of defining it as a basic specification as in Example 2.5. Another common use of the translate operation is to rename colimit specifications (see Section 3.4).
A translation is given by the keyword translate followed by a specification and a set of renaming rules, which indicate how the symbols of the specification are to be renamed. A renaming map is a one-to-one map used for copying a specification. If a renaming maps two sorts onto the same sort name, or two operations onto the same operation name, there will be multiple sorts or operations with the same name in the copied specification. Although this is not illegal, it is inconvenient in that references to these sorts or operations will be ambiguous. In a translation, the axioms are also rewritten to reflect the new names of the sorts and operations; however, the names of axioms, theorems, etc., remain the same. Also, the names of bound variables are unaffected by a translation, but changing the names of bound variables does not change the meaning of a formula anyway.
Translation Morphisms. The translate operation also constructs a translation morphism, which maps the elements of the original specification to the corresponding elements of the copied specification. This morphism can be denoted by translation-morphism, without giving its domain, codomain, or rules, in a context in which these can be inferred (see Section 2.2). This can happen, for instance, in presenting an interpretation (see page 70 for an example).
3.2 Import
Another simple operation for constructing specifications in Slang is import. The purpose of the import operation is to enrich a specification with new sorts, operations, axioms, and theorems. The operation is not technically necessary--a specification generated with import can also be constructed with other operations--but it is sometimes convenient.
Example 3.2 Reflexive Relations.
The specification REFLEXIVE-RELATION on page 34 is similar to BINARY-RELATION (see Example 2.5), except that it has an axiom and employs a different notation. In that example, we built the two specifications separately; however, when different specifications share structure in that way, it is wise to make the relationship explicit. For one thing, we save effort and reduce the chance of error, because we introduce each new concept once, not many times. Furthermore, any later change we make in the subspecification will be automatically reflected in the larger specification. These points will be evident in our larger examples.
In Example 3.1 of the previous section, the specification BINARY-RELATION was translated so that its notation was made consistent with that of REFLEXIVE-RELATION. We now use the import operation to add the additional axiom:
spec REFLEXIVE-RELATION is
import
translate BINARY-RELATION by
{br -> rr}
axiom reflexive is
(rr e e)
end-spec
This alternative specification for reflexive relations makes explicit the relationship with the binary relations.
Models and Definitional Extensions. As we have mentioned earlier, the model of a specification may be regarded as the class of objects it discusses. For example, the natural numbers with the relation <= may be regarded as a model for the specification BINARY-RELATION; so may the sets with the proper subset relation Ã. A model of a specification assigns a meaning to each of its sorts and operations so that each of its axioms will be true.
In the preceding example, the import mechanism was used to extend a theory, by adding an axiom that restricted the models. For example, the reflexive axiom restricted the models of the specification BINARY-RELATION, because some binary relations are not reflexive. The nonnegative integers with <= are a model for REFLEXIVE-RELATION--the sets with à are not.
Sometimes we may import a specification to define some new operations, without restricting the models. Such an operation is called a definitional extension. For example, let us extend the theory of binary relations by introducing the notion of the reflexive closure (rcl br) of a binary relation br.
spec REFLEXIVE-CLOSURE is
import BINARY-RELATION
op rcl : (E, E -> Boolean) -> (E, E -> Boolean)
definition of reflexive-closure is
axiom (iff ((rcl br) d e)
(or (br d e)(equal d e)))
end-definition
end-spec
Thus, the reflexive closure of the proper subset relation à is the subset relation Õ.
In this specification, we are not restricting the models of the specification BINARY-RELATION, because every binary relation has a reflexive closure. Thus this is a definitional extension of the binary relations.
The notion of definitional extension will be important when we begin to discuss refinement. (Section 4)
Note that in this specification we are defining a higher-order operation rcl, which is applied to other operations. Its type is
(E, E -> Boolean) -> (E, E -> Boolean)
This means that when applied to one binary relation, i.e., an operation of type
(E, E -> Boolean)
it yields another binary relation.
There can be only one import in a specification (but see the discussion ``Import Abbreviations''on page 52). A specification term containing an import declaration (as in the example above) stands for a specification which contains all the elements of the imported specification together with any sorts, operations, axioms, or theorems added in the term.
Import Morphisms. The import operation also constructs an import morphism which maps the elements of the imported specification to the corresponding elements of the importing specification. Rather than being spelled out explicitly, this morphism can be denoted simply by import-morphism in a context in which the domain and codomain can be inferred (see Section 2.2), e.g., in an interpretation. This will be illustrated on page 70.
3.3 Application: Families of Specifications
While it is always possible to build up a large specification directly, there are many advantages to building it modularly from smaller components, as we have remarked. For one, we can see the relationship between various specifications--what they have in common and how they differ. If instead of building up these specifications from scratch separately, we develop them in a tree-like hierarchy, we can see immediately which axioms the theories share and which serve to distinguish between them.
Example 3.3 Sets, Bags, and Sequences.
We need to develop three separate theories of finite collections of elements. These theories have a family resemblance. In each theory, all the elements are of the same sort and there is an empty collection and an insertion operation for introducing new elements to a collection. In each theory, every collection can be obtained by repeatedly inserting new elements to the empty collection. The theories differ, however, in whether the order of the elements or their multiplicity is regarded as significant.
In a set, neither order nor multiplicity is significant. Two sets are regarded as equal if they have the same elements, regardless of order or multiplicity. Thus, if E is the sort of upper-case letters, {X, Y}, {Y, X}, and {X, X, Y} are all the same set.
A bag is like a set but it makes a difference how many times an element occurs in a bag. Two bags are regarded as equal if they have the same elements with the same multiplicity; the order is insignificant. Thus the bag {{X, Y}} is the same as the bag {{Y, X}} but different from the bag {{X, X, Y}}.
In a sequence, both order and multiplicity are significant. Two sequences are equal if they have the same elements in the same order. Thus the three sequences [X, Y], [Y, X], and [X, X, Y] are distinct.
Rather than defining three separate specifications, we shall define a generic specification COLLECTION. In a collection, we do not say whether order or multiplicity is significant--that is unspecified. Thus we cannot prove that col(X, Y) and col(Y, X) are the same, but neither can we prove that they are distinct.
We shall then extend the theory of collections to obtain a specification SACK, in which order is not significant but it is not specified whether multiplicity is significant. Thus, we can prove that sack(X, Y) and sack(Y, X) are the same but we cannot prove whether sack(X, Y) or sack(X, X, Y)are the same or distinct. Maybe so, maybe not.
The theories for sets and bags are each extensions of the theory of sacks, obtained by introducing additional axioms. The theory of sequences, on the other hand, is a separate extension of the theory of collections.
Collections. The theory of collections is specified as follows:
spec COLLECTION is
sorts E, Col
const empty-col : Col
op insert-col : E, Col -> Col
constructors {empty-col, insert-col} construct Col
theorem decomposition is
(implies (not (equal c empty-col))
(ex (e d)(equal c (insert-col e d))))
end-spec
Here empty-col is the empty collection and (insert-col e c) is the operation that inserts a new element e into the collection c. The collection that we informally write as col(d, e) is denoted in the theory by the term
(insert-col d (insert-col e empty-col))
The constructor set expresses the property that every collection can be obtained by repeatedly applying the insertion operation, a finite number of times, to the empty collection and the elements of E. It corresponds to an induction principle. There are no other explicit axioms. The decomposition theorem, which follows, says that every nonempty collection can be decomposed into the result of applying the insertion function to an element and a collection.
The theory of collections is very weak: one of its models, in fact, is one in which all collections are equal to the empty collection.
Sacks. Here is the specification for the theory of sacks:
spec SACK is
import
translate COLLECTION a
by {Col -> Sack,
empty-col -> empty-sack,
insert-col -> insert-sack}
op in-sack? : E, Sack -> Boolean
axiom empty is
(not (in-sack? e empty-sack))
axiom in-sack is
(iff
(in-sack? e (insert-sack d s))
(or (equal e d)
(in-sack? e s)))
axiom exchange is
(equal
(insert-sack e (insert-sack d s))
(insert-sack d (insert-sack e s)))
theorem retention is
(in-sack? e (insert-sack e s))
theorem conservation is
(not (equal empty-sack (insert-sack e s)))
end-spec
Note that the specification is constructed by importing the specification for collections, translated to replace collection vocabulary with sack vocabulary. Therefore we implicitly have a constructor set and a decomposition theorem for sacks; the translated decomposition theorem reads
theorem decomposition is
(implies (not (equal s empty-sack))
(ex (e t)(equal s (insert-sack e t))))
(Actually we have changed the names of the variables c and d to s and t by hand to make the notation consistent with our other sack properties.)
We extend the translated specification by introducing a membership predicate in-sack?, for determining whether an element belongs to a sack. The axioms empty and in-sack define the predicate. A third axiom exchange asserts that the order in which elements are inserted into a sack is inconsequential.
The axioms empty and in-sack are not merely definitions of the membership predicate--they extend the theory and restrict its models. They imply, for instance, the retention theorem, that the result of inserting an element into a sack does indeed contain that element; and hence the conservation theorem, that the empty sack is distinct from the result of inserting an element into a sack, because the empty sack has no members but the result of the insertion has at least one. Consequently, in contrast with the theory of collections, there is no model for the theory of sacks in which all sacks are equal
The theory of sacks is still neutral about whether the multiplicity of the elements in a sack is significant--in some models it is, in others it isn't.
Sets. As before, the specification for the theory of sets is constructed by importing the theory of sacks, translated into appropriate vocabulary:
spec SET is
import
translate SACK
by {Sack -> Set,
empty-sack -> empty-set,
insert-sack -> insert-set,
in-sack? -> in-set?}
axiom condensation is
(equal (insert-set e (insert-set e s))
(insert-set e s))
theorem equality is
(iff (equal s t)
(fa (e) (iff (in-set? e s)(in-set? e t))))
end-spec
Any properties of sacks, such as the conservation theorem, automatically apply to sets, after translation. We introduce a single condensation axiom, to convey that inserting an element into a set twice in succession is the same as inserting it once. This, along with the translated sack axioms, is enough to imply the equality theorem, that two sets are equal if they have the same elements, regardless of order or multiplicity. The condensation axiom and the equality theorem do not hold for sacks.
Bags. The specification for bags, like the specification for sets, imports the specification for sacks but translates its vocabulary:
spec BAG is
import
translate SACK
by {Sack -> Bag,
empty-sack -> empty-bag,
insert-sack -> insert-bag,
in-sack? -> in-bag?}
axiom uniqueness is
(implies
(equal (insert-bag e b) (insert-bag e c))
(equal b c))
end-spec
Instead of the condensation axiom we had for sets, we introduce a uniqueness axiom, which says that if the results of inserting the same element into two bags are equal, the two bags must already be equal; this axiom holds for bags but not for sets. (For example, the inserting X into the unequal sets {Y} and {X, Y} yields the equal sets {X, Y} and {X, Y}.) The uniqueness axiom, along with the translated axioms for sacks, allows us to establish that two bags are equal if they have the same elements with the same multiplicity, regardless of order. We do not state this explicitly within the specification, because we haven't introduced the vocabulary for talking about multiplicity.
Sequences. Because order is significant in sequences, the specification is an extension of the theory of collections, not sacks:
spec SEQ is
import
translate COLLECTION
by {Col -> Seq,
empty-col -> empty-seq,
insert-col -> prepend}
axiom conservation is
(not (equal (prepend e s) empty-seq))
axiom uniqueness is
(implies (equal (prepend e s) (prepend d t))
(and (equal e d) (equal s t)))
end-spec
For historical reasons, the insertion operation for sequences is called prepend; it is thought of as the operation that adds an element to the very beginning of a sequence (although nothing in the specification requires that, it could just as well be the end or middle). Note that the conservation property, which was a theorem for sacks, shows up as an axiom for sequences; without it there would be models for the theory in which all sequences are equal to the empty sequence. The uniqueness axiom for sequences is stronger than the uniqueness axiom for bags: it says that the only way the results of any two insertion operations can be equal is for both the corresponding new elements and the two original sequences to be equal. For instance, inserting the element X into a sequence never yields the same result as inserting the distinct element Y into a sequence. The analogous property for bags is false; for instance, inserting X into the bag {{Y}} gives the same result as inserting Y into the bag {{X}}.
The specification for sequences contains no membership relation, but a predicate in-seq? can be introduced by a definitional extension. This is in contrast to the theory of sacks, in which the axioms for in-sack? were an essential part of the theory and restricted its models.
The entire family of theories we have developed is illustrated in Figure 5. In this figure, each arc is labeled with the operations and axioms needed to extend one theory to the next; each node is a theory and is annotated with the theorems it mentions.\
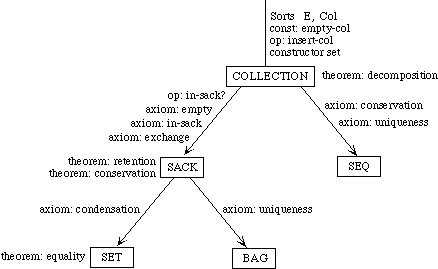
Figure 5: Family of Collection Theories
Note that a theorem associated with any of the nodes is also a theorem of any of its descendents, after translation into the appropriate vocabulary. This gives us a certain economy--for instance, we need to prove the decomposition theorem only once, not five or more times.
3.4 Colimit
The colimit operation is the fundamental method in Slang for combining specifications. The operation takes a diagram of specifications as input and yields a specification, commonly referred to as the colimit (or apex) of the diagram. The colimit contains all the elements of the specifications in the diagram, but elements that are linked by arcs in the diagram are identified in the colimit.
Each component specification of the diagram is linked to the colimit by a cocone (pronounced ``CO-cone'') morphism, which indicates how it may be viewed as a part of the colimit.
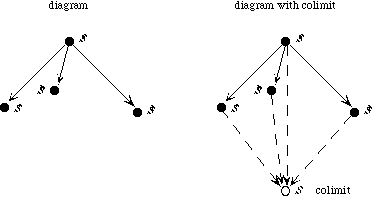
Figure 6: A Colimit
Figure 6 illustrates a colimit operation. On the left side is a diagram of four specifications, Sa through Sd, with morphisms between them. On the right side is the diagram with the colimit S. The dotted arrows represent cocone morphisms between the component specifications and the colimit.
Example 3.4 Preorders.
In the preorder diagram (Example 2.5), we indicated correspondences between elements of two specifications, REFLEXIVE-RELATION and TRANSITIVE-RELATION, by means of an intermediate specification, BINARY-RELATION. By applying the colimit operation to this diagram, we can combine these specifications, identifying the corresponding elements, to obtain a specification for PREORDER, a theory of the reflexive, transitive relations. The combined specification will contain both the reflexive and transitive axioms.
Let us recall the specification for the binary relations:
spec BINARY-RELATION is
sort E
op br : E, E -> Boolean
end-spec
Here is the specification for the reflexive relations, phrased so that it imports the binary-relation specification, as on page 40:
spec REFLEXIVE-RELATION is
import
translate BINARY-RELATION by
{br -> rr}
axiom reflexive is
(rr e e)
end-spec
And here is the specification for the transitive relations, phrased in the same way to import the binary-relation specification.
spec TRANSITIVE-RELATION is
import
translate BINARY-RELATION by
{br -> tr}
axiom transitive is
(implies (and (tr c d) (tr d e))
(tr c e))
end-spec
As in Example 2.5, let us compose these into a diagram:
diagram PREORDER-DIAGRAM is
nodes BINARY-RELATION, REFLEXIVE-RELATION, TRANSITIVE-RELATION
arcs BINARY-RELATION -> REFLEXIVE-RELATION :
{br -> rr},
BINARY-RELATION -> TRANSITIVE-RELATION :
{br -> tr}
end-diagram
We can now define a preorder, i.e., a reflexive, transitive relation, by taking the following colimit:
spec PREORDER is
colimit of PREORDER-DIAGRAM
This colimit is illustrated in Figure 7.
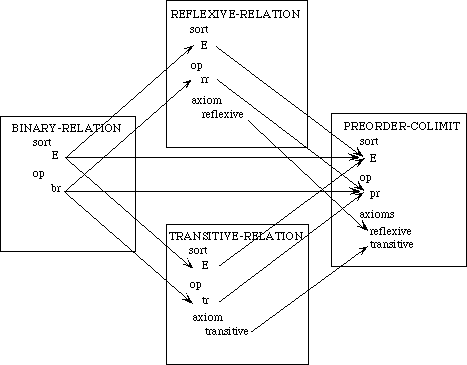
Figure 7: Colimit for PREORDER
The resulting specification PREORDER will have a single sort that identifies the separate sorts and operations indicated by the morphisms. It is equivalent to the following specification:
spec PREORDER is
sorts E
op pr : E, E -> Boolean
axiom reflexive is
(pr e e)
axiom transitive is
(implies (and (pr c d)(pr d e))
(pr c e))
end-spec
The observant reader will have noticed that in the specification PREORDER we have introduced new vocabulary; the relation operation is pr. To get this effect, we may compose the colimit operation with a translation:
spec PREORDER is
translate
colimit of PREORDER-DIAGRAM
by {br -> pr}
It is typical to follow a colimit operation with a translation in this way.
Informally, the colimit specification is a ``shared'' union of the specifications associated with each node of the original diagram. ``Shared'' here means that sorts and operations that are linked by the morphisms of the diagram are identified as a single sort and operation in the colimit specification. Thus the separate operations br, rr, and tr, which are linked by morphisms of the diagram, are identified as a single operation pr in the colimit.
Formally, given a diagram, the colimit operation creates a new specification, the colimit specification. It also creates a new cocone morphism from the specification at each node in the given diagram to the new colimit specification. In Figure 7, the arrows leading into the rightmost box, the PREORDER-COLIMIT, represent cocone morphisms.
The colimit specification and the cocone morphisms leading into it satisfy the property that the resulting diagram commutes. In other words, for every node in the diagram and for every sort or operation in the specification at that node, the translation of the sort or operation along any path leading from the node to the colimit specification is the same; thus, whatever path we follow from the operation br in the specification BINARY-RELATION, we reach the same operation in PREORDER-COLIMIT. Furthermore, the colimit specification only contains those sorts and operations which arise as the translations of some sort or operation in the specification at some node in the diagram.
Cocone Morphisms. As discussed just above, for each node, the colimit operation constructs a cocone morphism from the specification at that node in the given diagram to the colimit specification. These morphisms can be denoted by cocone-morphism from <node-name> in a context in which the codomain can be inferred (see Section 2.2); the domain is indicated by <node-name>.
Import Abbreviations. Slang provides abbreviations for two frequently occurring constructs involving colimits and imports
spec
import colimit of diagram
nodes <spec1>, <spec2>, ..., <specn>
end-diagram ...
end-spec
in which the diagram has no arcs, can be abbreviated as simply
spec import <spec1>, <spec2>, ..., <specn> ... end-spec
3.4.1 The Colimit Construction Algorithm
The colimit specification and the associated cocone morphisms are constructed using the standard union-find algorithm for computing the connected components of a graph. The disjoint union of the sorts and operations contained in the specifications at all the nodes in the diagram is formed; note that, if the same specification labels two different nodes in a diagram, then two copies of the sorts and operations in that specification are generated in the disjoint union. This set is partitioned into equivalence classes according to the mappings given by the morphisms that label the arcs in the diagram. Two sorts or operations are made equivalent (i.e., they are put into the same equivalence class) iff there is an arc whose morphism maps one into the other. The colimit specification contains one sort or operation corresponding to each equivalence class. The cocone morphism from the specification at each node in the diagram is the map that takes each sort or operation to the equivalence class that contains it.
In the presence of sort axioms, it is possible for the basic equivalence classes to contain multiple constructed sorts. Hence, when using sort axioms, you must ensure that no two distinct constructed sorts are made equivalent: this would violate the freeness restriction--see the discussion of sort axioms in Section 1.3 on page 17.
As a special case of the colimit operation, if a diagram consists of just nodes with no arcs between them, the colimit is the disjoint union of the specifications labeling the nodes of the diagram. In other words, the equivalence classes are all singletons.
3.4.2 Colimit to Merge Elements
We have used the colimit operation to combine separate theories; morphisms indicate what elements of the theories are to be identified. The colimit operation can be used to identify two sorts or operations in a single specification. This is illustrated in the following example.
Example 3.5 Binary Relations.
In our specification BINARY-RELATION, the domain and codomain of our relations were of the same sort E. Let us reconstruct this specification by assuming we have a specification BINARY-RELATION-DISTINCT, in which the domain and codomain may be of two different sorts, D and E respectively. We shall use the colimit operation to identify the two sorts D and E to obtain a specification equivalent to our BINARY-RELATION, in which the domain and codomain of a relation are of the same sort.
The more general specification for the binary relations, in which the domain and range may be distinct, is:
spec BINARY-RELATION-DISTINCT is
sorts D, E
op bd : D, E -> Boolean
end-spec
To identify the two sorts D and E, we introduce a specification ONE-SORT with only a single sort. This specification is as follows:
spec ONE-SORT is
sort X
end-spec
The sort X will be linked by two morphisms to D and E respectively; thus, all three sorts will be regarded as the same in the colimit. Actually, the colimit will have a single sort, the equivalence class {D,E,X}. This class may also be referred to by the aliases D, E, and X.
The colimit operation that combines these specifications is
spec BINARY-RELATION is
translate
colimit of
diagram
nodes ONE-SORT, BINARY-RELATION-DISTINCT
arcs ONE-SORT -> BINARY-RELATION-DISTINCT : {X -> D},
ONE-SORT -> BINARY-RELATION-DISTINCT : {X -> E}
end-diagram
by {bd -> br} colimit}
It is illustrated graphically in Figure 8.

Figure 8: Binary Relation Colimit Diagram
Note that, as we mentioned earlier, there are two morphisms from ONE-SORT to BINARY- RELATION-DISTINCT:
As a result, in the colimit, D and E are collapsed into a single sort. As we saw in the previous example, the vocabulary for the colimit (br instead of bd) is introduced in a subsequent translation phase.
3.4.3 Colimit to Instantiate Parameters
In our next example, we shall use the colimit operation to instantiate parameters.
Example 3.6 Sets of Pairs.
We have seen a specification for the theory of finite sets, in which the elements of the sets are all of the same sort E (Section 3.3on page 41). We shall now give a specification PAIR for pairs [d, e], where d and e are of sorts D and E, respectively. We shall then use the colimit operation to construct a specification SET-OF-PAIRS for sets whose elements are all pairs.
The specification for pairs, as on page 29, is as follows:
spec PAIR is
sorts D, E, Pair
op make-pair : D, E -> Pair
op first : Pair -> D
op second : Pair -> E
axiom (equal (first (make-pair d e)) d)
axiom (equal (second (make-pair d e)) e)
constructors {make-pair} construct Pair
theorem (equal p (make-pair (first p) (second p)))
end-spec
In this specification, the pairs are of sort Pair. The operation make-pair constructs a pair from two elements; the two functions first and second extract the first and second components, respectively, from a pair.
To combine these two theories, we want to make E, the sort of the elements of the sets, the same as Pair, the sort of the pairs. For this purpose, we introduce a third specification, the theory ONE-SORT we used in the previous example, to indicate the sorts that are to be identified. This was the specification with a single sort X and no operations or axioms. Two morphisms identify X with the sort E of SET and the sort Pair of PAIR, respectively.
The combination of the theories is achieved by the following colimit operation:
spec SET-OF-PAIRS is
translate
colimit of
diagram
nodes ONE-SORT, SET, PAIR
arcs
ONE-SORT -> SET : {X -> E},
ONE-SORT -> PAIR : {X -> Pair}
end-diagram
by {Set -> Set-of-Pairs,
empty-set -> empty-set-of-pairs,
insert-set -> insert-set-of-pairs,
in-set? -> in-set-of-pairs?}
We follow the colimit operation with a translation, so that the set operations in the colimit will be distinguished by the suffix set-of-pairs. Thus, the empty set in this specification is called empty-set-of-pairs. A diagram of the essentials of the colimit is given in Figure 9.
Figure 9: Set-of-Pairs Colimit Diagram
The specification obtained by taking the colimit is equivalent to one presented directly in Figure 10.
spec SET-OF-PAIRS is
sorts Set-of-Pairs, Pair, D2, D1
op in-set-of-pairs: Pair, Set-of-Pairs -> Boolean
op insert-set-of-pairs: Pair, Set-of-Pairs -> Set-of-Pairs
const empty-set-of-pairs: Set-of-Pairs
op second: Pair -> D2
op first: Pair -> D1
op make-pair: D1, D2 -> Pair
constructors {empty-set-of-pairs, insert-set-of-pairs}
construct Set-of-Pairs
constructors {make-pair} construct Pair
conjecture equality is
(fa (t s)
(iff
(equal s t)
(fa (e) (iff (in-set-of-pairs e s) (in-set-of-pairs e t)))))
axiom condensation is
(fa (s e)
(equal
(insert-set-of-pairs e (insert-set-of-pairs e s))
(insert-set-of-pairs e s)))
theorem conservation is
(fa (s e)
(not (equal empty-set-of-pairs (insert-set-of-pairs e s))))
theorem retention is
(fa (s e) (in-set-of-pairs e (insert-set-of-pairs e s)))
axiom exchange is
(fa (s d e)
(equal
(insert-set-of-pairs e (insert-set-of-pairs d s))
(insert-set-of-pairs d (insert-set-of-pairs e s))))
axiom in-sack is
(fa (s d e)
(iff
(in-set-of-pairs e (insert-set-of-pairs d s))
(or (equal e d) (in-set-of-pairs e s))))
axiom empty is
(fa (e) (not (in-set-of-pairs e empty-set-of-pairs)))
theorem decomposition is
(fa (c)
(implies
(not (equal c empty-set-of-pairs))
(ex (e d) (equal c (insert-set-of-pairs e d)))))
conjecture
(fa (x) (equal x (make-pair (first x) (second x))))
axiom (fa (x2 x1) (equal (second (make-pair x1 x2)) x2))
axiom (fa (x2 x1) (equal (first (make-pair x1 x2)) x1))
end-spec
Figure 10: Specification of Sets of Pairs Defined Directly
This specification combines axioms from the two specifications. Note that, as our specifications grow larger, it becomes more economical to use the colimit and other specification-constructing operations than to define specifications directly.
3.4.4 Qualified Names
As explained above, the sorts and operations in a colimit specification are equivalence classes. Each such sort or operation inherits all the names of its elements as aliases, and may be referred to (in a specification which imports the colimit) by any one of these aliases. However, it is frequently the case that the name of an element of an equivalence class does not uniquely determine the class. This can occur when more than one node in the diagram for the colimit is associated with the same specification.
In such a case, to denote these equivalence classes, qualified names are used. A simple qualified name is a name of the form <qualifier>.<name>. The qualifier is the name of a node in the diagram used to construct the colimit. The denotation of such a qualified name is the equivalence class that contains the sort or operation denoted by the unqualified name in the specification attached to the qualifier node. Qualified names need not be used if a sort (or operation) name alone uniquely identifies an equivalence class. This is true even if the equivalence class contains many names.
Example 3.7 Double Binary Relations.
To illustrate the need for qualified names, consider the following specification, in which two binary relations are defined on the same sort.
spec DOUBLE-BINARY-RELATION is
colimit of
diagram
nodes A: ONE-SORT,
B: BINARY-RELATION,
C: BINARY-RELATION
arcs A -> B : {X -> E},
A -> C : {X -> E}
end-diagram
Here we take the colimit of a diagram that contains two nodes labeled by the same specification, that of a binary relation. To collapse the sorts in the two copies of the binary relation specification into one, we introduce a third node, labeled with the specification ONE-SORT. Two morphisms map the sort X of ONE-SORT into the two copies of the sort E of BINARY-RELATION, forcing them to be the same; the two copies of the relation br are not linked, and hence are taken to be distinct.
The colimit specification will contain a single sort, the equivalence class {E,X}, with aliases E and X, and two operations with the same name and sort:
br : {E,X}, {E,X} -> Boolean
If, in another specification that imports DOUBLE-BINARY-RELATION, we want to refer to these operations, we have to use qualified names, B.br and C.br, to distinguish the two copies. For example, we could rename these operations and require that they be inverses:
spec FAMILY is
import
translate DOUBLE-BINARY-RELATION
by {E -> People,
B.br -> parent,
C.br -> child}
axiom (iff (parent x y) (child y x))
end-spec
In general, to handle the case of the specification attached to a node being itself a colimit, cascaded qualifiers are allowed. That is, the most general form of a reference in Slang is
<qualifier>.<qualifier>....<qualifier>.<name>
Such a reference is resolved by starting with the outermost qualifier and proceeding inwards. That is, the outermost qualifier must be the name of a node in the diagram used to construct the current colimit; that node must itself correspond to a colimit; the second qualifier must be the name of a node in the diagram used to construct that colimit; and so forth.
While qualified names can be used to refer to a sort or operation of a colimit specification, the system does not display specifications using qualified names. If an equivalence class with more than one element is formed in a colimit specification, it is printed as an equivalence class, i.e., as the set containing all of the names of the sorts (operations) in the class. If the class contains just a single name, that name is printed and the set brackets are suppressed.
3.4.5 Consistency of Colimits
It is possible to use the colimit operation to construct an inconsistent theory, even if all the component specifications in the diagram are themselves consistent. This can happen when the axioms from the component theories contradict each other.
For example, suppose we want to construct a theory that combines the properties of sets and sequences; the elements of the sets and sequences will be bits, zero and one. We specify the combination by the following colimit:
spec SEQ-SET is
import
colimit of diagram
nodes COLLECTION, SEQ, SET, ONE-SORT, BIT
arcs
ONE-SORT -> BIT : {X -> Bit},
ONE-SORT -> COLLECTION : {X -> E},
COLLECTION -> SEQ :
{Col -> Seq,
empty-col -> empty-seq,
insert-col -> prepend},
COLLECTION -> SET :
{Col -> Set,
empty-col -> empty-set,
insert-col -> insert-set}
end-diagram
theorem (equal one zero)
theorem (not (equal one zero))
end-spec
The diagram for the colimit of this specification is illustrated as follows:
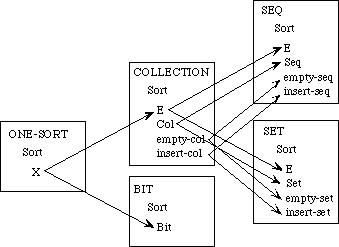
Note that the sequence and set specifications have been linked together via the collection specification, so that the respective elements, collections, empty collections, and insertion functions of these specifications have been identified. (The identification of the elements in the three specifications does not have to be spelled out explicitly in the morphisms of the diagram, because they happen to have the same name E.) Hence collections in the colimit have properties of both sequences and sets. Also the elements of the three specifications are linked, via the specification ONE-SORT, with the bits; the specification for bits is as follows:
spec BIT is
sort Bit
op zero : Bit
op one : Bit
axiom (not (equal zero one))
constructors {zero, one} construct Bit
end-spec
Thus the elements of the sequences and sets are zero and one; the axiom ensures that these elements are distinct, and the constructor set guarantees that there are no others.
The inconsistency of the resulting specification is demonstrated by including two contradictory theorems. That zero and one are not equal is the axiom of the specification BIT, which has been inherited via the colimit mechanism. That they are equal follows because, by axioms of the sets, col (zero, one) is equal to col (one, zero). But then, by the uniqueness axiom for sequences, zero equals one.
Note that if we had not linked the elements to the bits or some other specification with at least two elements, no contradiction would have been obtained. We could use the same kind of argument to show that any two elements are equal, i.e., that the sort of elements actually has only one element, but that is not a contradiction.
Although there is no general mechanism for checking consistency of a colimit, Specware can detect inconsistencies in some cases by invoking the system's theorem prover. Furthermore, if we use Specware to generate code for a specification (Section 6), we must find a refinement into one of the built-in theories; assuming that these theories are themselves consistent, that implies that the specification is also consistent.
Part II Refinement Constructs in Specware
The principal technique for software design and development in Specware is a process of refinement of a problem (or source) specification into a solution (or target) specification. Refinements replace behavioral constraints with algorithms and abstract data structures with implementations. Source and target specification as well as the refinements between them are precise, formal objects. Slang's refinement constructs, introduced and defined in subsequent chapters, address three important aspects of refinement:
4 Overview of Refinement
A morphism maps each element (e.g., a sort or operation) of the source specification into an element that exists explicitly in the target; this notion is too restrictive to serve as the basis for all refinement. Interpretations generalize morphisms to capture a more applicable notion of specification refinement. In particular, we may map elements in the source into elements that do not exist explicitly in the target, but that are introduced by definitions. These new elements are introduced in an intermediate specification known as a ``mediator''.
In Specware, refinement of specifications proceeds by induction on the specification structure; in other words, we define the refinement of a structured specification, which has been defined by specification-constructing operations, in terms of the refinements of its components.
The next section gives an overview of refinement of basic specifications and the following section gives an overview of the refinement of structured specifications. These notions are more fully discussed in Section 5. It will then be seen that refinement of structured specifications requires a systematic lifting of specification notions (specifications, specification morphisms, and specification-constructing operations) to corresponding refinement notions (interpretations, interpretation morphisms, and interpretation-constructing operations).
Convention. All the morphisms and diagrams we treated in Part I were specification morphisms and diagrams. In Part II, we shall encounter other kinds of morphisms and diagrams, e.g., interpretation morphisms and interpretation diagrams. We have the convention, however, that when ``morphism'' or ``diagram'' is used without a qualifier, it means ``specification morphism'' or ``specification diagram,'' respectively. Other uses are qualified with the kind of objects involved.
4.1 Refinement of Basic Specifications
The basic refinement construct in Slang is an interpretation (see Section 5). Interpretations generalize morphisms as follows.
We have seen (Section 2.2) that a morphism from specification S to specification T maps the sorts, operations, and axioms of S into sorts, operations, and theorems, respectively, of T. We have also seen (Section 3.2) that a definitional extension of T is a specification that contains all the sorts, operations, and axioms of T plus definitions of additional sorts and operations. An interpretation from S to T, then, is a morphism from S into a mediator, often called S-as-T, which is a definitional extension of T. We shall then also say that T is a refinement of S. The words ``refinement'' and ``interpretation'' are synonymous.
For example, in the next section we implement sets in terms of bags. Under the interpretation we construct, each set corresponds to a bag with no repeated elements. In the basic specification for bags, there is no sort corresponding to bags with no repeated elements. Therefore, we define this sort in a mediator that is a definitional extension of the specification for bags. The morphism then maps the sort of sets in the source into this new sort in the mediator.
Every morphism from S to T is an interpretation, because T can be regarded as a definitional extension of itself. But not every interpretation is a morphism, because some elements of S may map into sorts or operations of the definitional extension of T that are not in T itself. It will turn out that interpretations, like morphisms, are closed under sequential composition--the result of following one interpretation with another is a refinement of the original specification. This allows us to follow one refinement by another.
4.2 Refinement of Structured Specifications
We systematically exploit the specification structure to construct interpretations for complex specifications.
Colimit Refinement The colimit of a diagram of interpretations yields an interpretation from a colimit of the interpretations sources to a colimit of the interpretation targets.
Translation Refinement If specification T is a translation of specification S, then there is a translation of any interpretation with source S into an interpretation with source T.
Import Refinement If specification T imports specification S, it is not in general possible to construct an interpretation for T from an interpretation for S. However, it is possible if the import morphism is a definitional extension.
5 Interpretations and their Composition
We first introduce the syntax for interpretations in Slang and illustrate with some examples. Subsequently, we discuss the sequential (vertical) and parallel (horizontal) composition of interpretations. The parallel compositions, i.e., the gluing of interpretations from pieces, requires us to consider interpretation morphisms and a generalization of interpretations, interpretation schemes. Parallel composition requires that the refinement components be compatible. This compatibility notion is made precise in Section 5.4.
Before we give the definition of an interpretation, let us give a more technical treatment of the notion of a definitional extension.
5.1 Definitional Extensions
An interpretation from S into T is a morphism from S into a definitional extension of T. We have already introduced definitional extensions informally (Section 3.2). Now let us go over the same material more formally.
For two specifications S and T, a morphism S to T is a strict definitional extension if it is injective (one-to-one) and if every sort or operation of T that is outside the image of the morphism is defined in terms of elements that are inside the image. A definitional extension is a strict definitional extension optionally composed with a specification isomorphism. (An isomorphism is an injection whose image includes all the elements of the specification, e.g., a translation.)
If m: S ->T is a definitional extension, we also say that T is a definitional extension of S. If T is a definitional extension of S, then T is consistent if and only if S is consistent. Also, any translation of a specification is a definitional extension of that specification.
A specification and its definitional extensions are in some sense equivalent--they define the same theories and have the same models, except for changes in vocabulary--but the extensions will contain explicit definitions for new sorts and operations.
In the present implementation, Specware determines whether a morphism is a definitional extension by using syntactic properties of definitions. A definitional extension will graphically be shown as

In the following figure, suppose T' is a colimit of the diagram containing the morphisms m and n (and hence S, S', and T); we call such a configuration a pushout and indicate it with the marking ``po.'

Pushouts preserve definitional extensions in the sense that if m is a definitional extension, then the opposite (cocone) morphism m' is also a definitional extension. Furthermore, definitional extensions are closed under (sequential) composition--the composition of two definitional extensions is also a definitional extension. Both properties, preservation by pushouts and closure under composition, will be needed for sequential composition of interpretations.
5.2 Basic Interpretations
Now that we have discussed definitional extensions, we can give the definition of an interpretation.
Definition 5.1: Interpretation.
An interpretation with domain (or source) specification S and codomain (or target) specification T has several components:
We require that the target morphism t be a definitional extension--hence t is one-to-one and any axioms of the mediator that are outside of the image of t merely define new sorts or operations without restricting the models. We also allow the mediator to employ a different vocabulary. We may also say that the mediator itself is a definitional extension of the target--this agrees with our terminology in the previous subsection.
Typically, the mediator S-as-T will import the target T and add whatever definitions are necessary to provide images or representations for the elements of S. If the target morphism were not a definitional extension, there would be no guarantee that we could use the interpretation to provide implementations for elements of the source specification.
A prototypical example of a named Slang interpretation is of the form
interpretation s-to-t: S => T is
mediator S-as-T
dom-to-med s
cod-to-med t
Note the use of the double arrow instead of a single arrow, to indicate an interpretation rather than a morphism.
A graphical rendering of this construct is as follows:
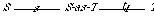
Because any specification can be regarded as a definitional extension of itself, any morphism can be the source morphism of an interpretation whose target morphism is the identity. In this sense, the notion of interpretation is considered to be a generalization of the notion of a morphism. Usually, though, we must extend the target specification with definitions of new sorts and operations to serve as images of the elements of the source specification.
Example 5.2 Interpretation of Sets as Bags.
Here is a paradigmatic use of an interpretation to refine a data type specification: the representation of sets by bags. Both the set and the bag specifications describe finite unordered collections of elements. While it is not meaningful to ask how many times an element occurs in a set, it is meaningful in a bag (see Families of Specifications, Example 3.3).
Our specification for sets was given on page 45. It provided a constant empty-set, an operation insert-set for adding a new element into a set, and a predicate in-set- for determining whether an element belongs to a set. Our specification for bags was given on page 45. It provides a constant empty-bag, an operation insert-bag, and a predicate in-bag- analogous to those for sets.
We shall represent sets as bags in which no elements are duplicated; for example, the set {X, Y, Z} will be represented as the corresponding bag {{X, Y, Z}}. We cannot simply map Set into Bag, empty-set into empty-bag, insert-set into insert-bag, and so forth, because the condensation axiom for sets, which says that inserting an element twice in succession into a set is the same as inserting it once, will then translate into a sentence that is not true of bags. Instead, our specification for bags is augmented in the mediator with a new sort, Set-as-Bag, which corresponds to bags with no duplicated elements. We also introduce operations on this sort that allow us to mimic the set operations. The axioms for sets will be translated into sentences that do hold for the new sort and operations. The extended specification, SET-AS-BAG, is given in Figure 11.
spec SET-AS-BAG is
import BAG
sort Set-as-Bag
op no-dup-bag? : Bag -> Boolean
definition of no-dup-bag? is
axiom (no-dup-bag? empty-bag)
axiom (iff (no-dup-bag? (insert-bag e b))
(and (not (in-bag? e b)) (no-dup-bag? b)))
end-definition
sort-axiom Set-as-Bag = Bag | no-dup-bag?
op bag-of-s-as-b : Set-as-Bag -> Bag
definition of bag-of-s-as-b is
axiom (equal bag-of-s-as-b (relax no-dup-bag?))
end-definition
const empty-s-as-b : Set-as-Bag
op insert-s-as-b : E, Set-as-Bag -> Set-as-Bag
op in-s-as-b? : E, Set-as-Bag -> Boolean
definition of empty-s-as-b is
axiom (equal (bag-of-s-as-b empty-s-as-b) empty-bag)
end-definition
definition of insert-s-as-b is
axiom (implies (in-bag? e (bag-of-s-as-b sb))
(equal (bag-of-s-as-b (insert-s-as-b e sb))
(bag-of-s-as-b sb)))
axiom (implies (not (in-bag? e (bag-of-s-as-b sb)))
(equal (bag-of-s-as-b (insert-s-as-b e sb))
(insert-bag e (bag-of-s-as-b sb))))
end-definition
definition of in-s-as-b? is
axiom (equal (in-s-as-b? e sb)
(in-bag? e (bag-of-s-as-b sb)))
end-definition
constructors {empty-s-as-b, insert-s-as-b} construct Set-as-Bag
end-spec
Figure 11: Specification for Sets Represented as Bags
In this specification, we introduce a predicate no-dup-bag? to determine whether a bag has no multiple occurrences of elements. That predicate is used to define Set-as-Bag, the subsort of bags that satisfy no-dup-bag?. We define bag-of-s-as-b to be the function (relax no-dup-bag?), which maps x viewed as an element of the subsort Set-as-Bag into x viewed as an element of Bag.
We then introduce a constant and two operations on the new subsort--these are to serve as ``implementations'' for empty-set, insert-set, and in-set?, respectively. For instance, the constant empty-s-as-b is defined to be the empty bag, viewed as an element of the subsort. Finally we introduce a constructor set for Set-as-Bag, to serve as the image for the constructor set of the set specification.
Now that we have augmented the specification for bags, we can define an interpretation from sets into bags. The mediator of this specification will be the augmented specification, SET-AS-BAG. The source morphism, which maps the source into the mediator, will be
morphism SET-TO-BAG : SET -> SET-AS-BAG is
{Set -> Set-as-Bag,
empty-set -> empty-s-as-b,
insert-set -> insert-s-as-b,
in-set? -> in-s-as-b?}
The target morphism, which maps the target into the mediator, will be simply the import morphism (see ``Import morphisms'' in Section 3.2); this is possible because the mediator imports the bag specification, which is the target.
Therefore our entire interpretation is
interpretation SET-TO-BAG : Set => Bag is
mediator SET-AS-BAG
dom-to-med SET-TO-BAG
cod-to-med import-morphism
Note that we have chosen to give the same name to the morphism and the interpretation; this is legal because morphisms and interpretation have separate name spaces; which meaning is intended is clear from context. We could have said {}instead of import-morphism; this would give the same result because the import morphism maps each element of the target into the same element in the mediator. However, if there were more than one element with the same name, it would be ambiguous to say {}.
Example 5.3 Interpretation of Bags as Sequences.
In our next example, we refine bags into sequences. This example illustrates the use of a quotient sort--each bag is mapped into an equivalence class of sequences, all of them permutations of each other. For example, the bag {{X, Y}} will be mapped into a class of two sequences, [X, Y] and [Y, X]. But the example is also of interest because we shall subsequently compose it with our previous refinement, from sets to bags--our first example of the (sequential) composition of interpretations. The composition will then refine sets into sequences. For example, the set {X, Y} will be represented by the equivalence class of two sequences, [X, Y] and [Y, X]. If we have an implementation for sequences, the composition will give us an implementation for sets.
Our specification for sequences was given in Section 3.3. Note that we cannot simply represent bags as sequences. Because the order of the elements in bags is irrelevant but the order of the elements in sequences is not, such an identification would result in an inconsistency--the exchange axiom for sacks and bags would map into an untrue sentence about sequences. Instead, just as we did when we represented sets as bags, we augment the sequence specification to include sorts and operations that allow us to mimic bags and bag operations. The extended specification, BAG-AS-SEQ, is given in Figure 12.
In this specification, we introduce a function count(x s) to count how many times the element x occurs in the sequence s. Rather than returning a nonnegative integer n as the answer--we have not imported a specification for the nonnegative integers--we return a sequence containing exactly n occurrences of x. Thus
(count X ([X, X, Y]) = [X, X]
We then define a predicate perm? that determines whether two sequences are permutations of each other. It does this using the count function to see if every element occurs exactly the same number of times in each sequence. This defines an equivalence relation on the sequences.
The sort Bag-as-Seq is then defined to be the quotient of the sequences by the permutation relation. The function b-as-s-of-seq is defined to be the quotient function that maps each sequence into its corresponding equivalence class.
We can then define the constant empty-b-as-s, the function insert-b-as-s, and the predicate in-b-as-s? to be the analogues for equivalence classes to empty-bag, insert-bag, and in-bag?, respectively, for bags. Each of these elements of the augmented specification for sequences will serve as the implementation of its analogue for bags. Because we have not introduced a membership function in-seq? into our specification for sequences, we must define the implementation predicate in-b-as-s? explicitly in the mediator. We also introduce a constructor set for Bag-as-Seq, to serve as the image for the constructor set for Bag.
Next we define a morphism mapping each element of the specification for bags into its corresponding implementation in the augmented specification for sequences.
morphism BAG-TO-SEQ : BAG -> BAG-AS-SEQ is
{Bag -> Bag-as-Seq,
empty-bag -> empty-b-as-s,
insert-bag -> insert-b-as-s,
in-bag? -> in-b-as-s?}
Our interpretation from bags to sequences is then
interpretation BAG-TO-SEQ : BAG => SEQ is
mediator BAG-AS-SEQ
dom-to-med BAG-TO-SEQ
cod-to-med import-morphism
Note that, as before, we could replace import-morphism by{}.
spec BAG-AS-SEQ is
import SEQ
op count : E, Seq -> Seq
definition of count is
axiom (equal (count e empty-seq) empty-seq)
axiom (equal (count e (prepend e s)) (prepend e (count e s)))
axiom (implies (not (equal e d))
(equal (count e (prepend d s)) (count e s)))
end-definition
op perm? : Seq, Seq -> Boolean
definition of perm? is
axiom (iff (perm? s t)
(fa (e) (equal (count e s) (count e t))))
end-definition
sort Bag-as-Seq
sort-axiom Bag-as-Seq = Seq/perm?
op b-as-s-of-seq : Seq -> Bag-as-Seq
definition of b-as-s-of-seq is
axiom (equal b-as-s-of-seq (quotient perm?))
end-definition
const empty-b-as-s : Bag-as-Seq
op insert-b-as-s : E, Bag-as-Seq -> Bag-as-Seq
op in-b-as-s? : E, Bag-as-Seq -> Boolean
definition of empty-b-as-s is
axiom (equal empty-b-as-s (b-as-s-of-seq empty-seq))
end-definition
definition of insert-b-as-s is
axiom (equal (insert-b-as-s e (b-as-s-of-seq s))
(b-as-s-of-seq (prepend e s)))
end-definition
definition of in-b-as-s? is
axiom (not (in-b-as-s? e empty-b-as-s))
axiom (iff (in-b-as-s? e (insert-b-as-s d bs))
(or (equal e d) (in-b-as-s? e bs)))
end-definition
constructors {empty-b-as-s, insert-b-as-s} construct Bag-as-Seq
end-spec
Figure 12: Specification for Sequences Augmented to Represent Bags
We now introduce a couple of interpretations that are of some interest in their own right and will be used in subsequent examples
Example 5.4 Interpretation of Sequences as Arrays.
In our next example, we shall implement sequences as arrays. Our arrays are actually one-dimensional vectors of entries a[0], . . ., a[n-1]. Sequences will be represented as arrays in reverse order; in other words, the first element of the sequence will be the last element of the array, and vice versa. This is because it is easier to add an element to a sequence at the beginning, via the operation prepend, but it is easier to add an element to an array at the end.
We shall relegate the full specification for arrays to Appendix E, page 160. The array specification imports a specification NAT for the nonnegative integers (see Appendix D, page 158) to provide the indices. As we have seen, arrays are indexed from 0 to n-1, where n is the size of the array, just the way the floors of European buildings are numbered. We distinguish between ordinary static arrays (in the specification ARRAY), whose size is fixed, and dynamic arrays (in the specification DYNAMIC-ARRAY), which can be extended. To implement sequences we use dynamic arrays, so that we can always add new elements to the end.
Some of the operations in the specification of static arrays are:
-
make-array: The function (make-array n e) constructs an array of size n, each of whose elements is initialized to e.
-
access-array: The function (access-array a i) returns the ith element (``a[i]'') of the array a. The integer i must be within the bounds of the array, that is, between 0 and n-1 inclusively, where n is the size of a.
-
update-array: The function (update-array a i e) returns a new array, which is identical to a except that its ith element is e. Again the integer i must be within the bounds of the array.
Dynamic arrays are an extension of static arrays. Some additional operations in the specification of dynamic arrays are:
-
empty-array: The constant empty-array is the array of size 0, with no elements.
-
extend-array: The function (extend-array a e) returns a new array, which is identical to a except that it is one element larger, of size n+1; its final (nth) element is e.
To implement basic sequences as (dynamic) arrays, we must augment the array specification with array operations empty-s-as-a and prepend-s-as-a that mimic the sequence operations empty and prepend, respectively. The constant empty-s-as-a is identified with the constant empty-array; the function prepend-s-as-a is defined in terms of the array function extend-array. The resulting mediator specification SEQ-AS-ARRAY is as follows:
spec SEQ-AS-ARRAY is
import translate DYNAMIC-ARRAY
by {empty-array -> empty-s-as-a}
op prepend-s-as-a : E, Array -> Array
definition of prepend-s-as-a is
axiom (equal
(prepend-s-as-a e a)
(extend-array a e))
end-definition
constructors {empty-s-as-a, prepend-s-as-a} construct Array
end-spec
The operation prepend-s-as-a, which will correspond to the operation prepend, places the new element e at the end of the array rather than the beginning. If we visualize sequences and arrays in the usual way, this has the effect of reversing the order of a sequence when it is represented as an array.
The interpretation that maps basic sequences into arrays is then simply
interpretation SEQ-TO-ARRAY : SEQ => DYNAMIC-ARRAY is
mediator SEQ-AS-ARRAY
dom-to-med {Seq -> Array,
empty-seq -> empty-s-as-a,
prepend -> prepend-s-as-a}
cod-to-med {empty-array -> empty-s-as-a} to-array}
Example 5.5 Interpretation of Finite Sets as Bit Vectors.
We have already seen an interpretation from sets into bags: now we shall see another implementation for sets, as bit vectors.
We represent sets of sort E, where E is finite, by bit vectors of size k, where k is the number of elements of sort E. If we number all the elements of sort E as e0 through ek-1, a set s will be represented by a bit vector v, where e1 belongs to s if and only if the ith element of the bit vector is 1. This is a practical way of representing sets if E is not too large.
For instance, if E is the integers from 0 through 7, numbered in order, the bit vector [0, 1, 0, 1, 0, 0, 1, 0], in which the first, third, and sixth elements are 1, represents the set {1, 3, 6}. This is illustrated in the following display:
We shall regard bit vectors as arrays whose elements are bits. Because we shall not need to make the bit vectors longer, we may use static rather than dynamic arrays. We have already seen the specification for sets in Section 3.3, page 41; the specification for static arrays is in Appendix E, page 160. The specification for bit vectors also depends on the specification for bits, which was given in Section 3.4.5, page 60. It says that there are two, and only two, distinct bits, denoted by zero and one.
A bit vector, then, is an array whose elements are of sort Bit:
spec BIT-VECTOR is
colimit of
diagram
nodes ONE-SORT, ARRAY, BIT
arcs ONE-SORT -> ARRAY : {X -> E},
ONE-SORT -> BIT : {X -> Bit}
end-diagram
Although we cannot make static arrays longer, our specification for static arrays, and hence our specification for bit vectors, allows arrays of all different sizes. We shall want to refine sets of elements of sort E into bit vectors all of the same size as E. Under this refinement, E will be identified with a sort of those nonnegative integers less than the size of E; each element of sort E will be identified with a different number. For this reason, we augment the bit-vector specification, obtaining a new specification BIT-VECTOR-FIXED, which describes bit vectors all of the same size, size-vector.
The full specification BIT-VECTOR-FIXED is given in the appendix (Section E, page 160). It contains the constant size-vector, the length of a bit vector, and a sort Interval, defined by the sort axiom
Interval = Nat | in-interval?
Here the predicate in-interval? holds for nonnegative integers strictly less than size-vector. The sort Interval will serve as the implementation for E under the interpretation.
The sort Bit-Vector-Fixed is then defined by the sort axiom
Bit-Vector-Fixed = Array | of-given-size?
Here the predicate of-given-size holds for arrays whose size is exactly size-vector.
Counterparts of ordinary array operations are then defined for fixed bit vectors: update-bvf, access-bvf, and others; the definitions relate the bit-vector operations and the corresponding array operations via the operator relax.
To implement finite sets as bit vectors, we augment the fixed-bit-vector specification to mimic the set operations. The empty set is the fixed bit vector each of whose elements is 0. To insert an element into a set, we assign the corresponding bit in the bit vector to 1. To test if an element is in the set, we see if the corresponding bit is 1.
spec SET-AS-BIT-VECTOR-FIXED is
import BIT-VECTOR-FIXED
const empty-s-as-bvf : Bit-Vector-Fixed
definition of empty-s-as-bvf is
axiom (equal empty-s-as-bvf (make-bvf BIT.zero))
end-definition
op insert-s-as-bvf : Interval, Bit-Vector-Fixed
-> Bit-Vector-Fixed
definition of insert-s-as-bvf is
axiom (equal (insert-s-as-bvf i v)
(update-bvf v i BIT.one))
end-definition
op in-s-as-bvf? : Interval, Bit-Vector-Fixed -> Boolean
definition of in-s-as-bvf? is
axiom (iff (in-s-as-bvf? i v)
(equal (access-bvf v i) BIT.one))
end-definition
constructors {empty-s-as-bvf, insert-s-as-bvf} construct
Bit-Vector-Fixed
end-spec
The constant empty-s-as-bvf is defined to be the array of length size-vector all of whose elements are zero. Note that the definition refers to BIT.zero to distinguish it from NAT.zero.
The operation insert-s-as-bvf implements the operation of inserting the element i into the set represented by the bit vector v by setting the ith element of v to one.
The operation in-s-as-bvf? implements the membership predicate; it tests if i is in the set represented by v by checking whether the ith bit of v is one.
The specification contains a constructor set to serve as the image of the constructor set for the sets. It corresponds to an induction axiom that asserts that any fixed bit vector can be obtained by successively applying the insertion function to the empty bit vector.
The interpretation that maps finite sets into bit vectors is then
interpretation SET-TO-BIT-VECTOR-FIXED :
SET => BIT-VECTOR-FIXED is
mediator SET-AS-BIT-VECTOR-FIXED
dom-to-med
{E -> Interval,
Set -> Bit-Vector-Fixed,
empty-set -> empty-s-as-bvf,
insert-set -> insert-s-as-bvf,
in-set? -> in-s-as-bvf?}
cod-to-med import-morphism
5.3 Sequential Composition of Interpretations
Sequential composition allows us to follow one interpretation with another; in this way, we can develop a system by successive refinement of its specification. But it is not immediately obvious that the composition of two interpretations is an interpretation. Why? What is the mediator of the composed intepretation? What is its target morphism and why is it a definitional extension? These questions are answered in this section; we also provide an example.
Definition 5.6: Sequential (Vertical) Composition of Interpretations.
Suppose rr1 and rr2 are two interpretations such that rr1 : R=> S and rr2 : S => T. Then their sequential composition rr1 ; rr2 : R => T is indicated by the vertical arrows in the following diagram:
Diagrams are assumed to be commutative unless stated otherwise. The left diagram is a summary--the right one provides details. The double arrows in the left diagram indicate interpretations; the single arrows in the right diagram indicate morphisms. In the left figure, the vertical arrow denotes the sequential composition of the two diagonal arrows.
Let us consider the right-hand figure, which shows the mediators and the source and target morphisms of each of the three interpretations. Here the marking ``po'' indicates a pushout square; that is, the mediator R-as-S-as-T of the composed interpretation is a colimit of the two morphisms in the square whose source is S. The upper of these morphisms, from S into R-as-S, is a definitional extension; it is the target morphism of the first of the given interpretations, rr1.
The source and target morphisms of the composed interpretation, which are the vertical arrows that lead into the new mediator, are defined to be the composition of the morphisms of the adjacent diagonal arrows. In particular, the upward arrow, from T to R-as-S-as-T, which represents the new target morphism, is the composition of the morphisms for the diagonal arrow from T to S-as-T and the diagonal arrow from S-as-T to R-as-S-as-T.
Both of these diagonal morphisms are definitional extensions: the morphism from T to S-as-T is the target morphism of the second of our given interpretations, rr2, and the morphism from S-as-T to R-as-S-as-T is opposite a definitional extension in our pushout square (see page 67). That their composition is also a definitional extension follows because definitional extensions are closed under composition. Therefore, the upward arrow is a proper target morphism for the new interpretation.
Sequential composition of interpretations facilitates incremental, layered refinement; this is illustrated in the following example.
Example 5.7 Interpretation of Sets as Sequences
As an example of the sequential composition of two interpretations, consider the interpretation of sets as bags in Example 5.2, page 70, together with the interpretation of bags as sequences in Example 5.3, page 72.
These two interpretations can be composed to yield an interpretation from sets to sequences. In the notation of the previous discussion, we simply take R to be SET, S to be BAG, and T to be SEQ. We obtain the following configuration:

Sequential composition of interpretations is most easily performed thoughtlessly via Specware's graphical facilities, but here we describe it textually. The mediator for the composed interpretation, SET-AS-BAG-AS-SEQ, is obtained by taking the following colimit:
spec SET-AS-BAG-AS-SEQ is
colimit of
diagram
nodes BAG, SET-AS-BAG, BAG-AS-SEQ
arcs BAG -> SET-AS-BAG : import-morphism,
BAG -> BAG-AS-SEQ : BAG-TO-SEQ
end-diagram
This is the pushout square we referred to in the previous discussion.
The source morphism for the composed interpretation is the composition of two morphisms:
Their composition is equal to the following morphism:
morphism SET-TO-SEQ : SET -> SET-AS-BAG-AS-SEQ is
{Set -> Bag-as-Seq,
empty-set -> empty-b-as-s,
insert-set -> insert-b-as-s,
in-set? -> in-b-as-s?}
The target morphism for the composition is also the composition of two morphisms:
Each of these morphisms is equal to the morphism {}, with the appropriate domain and codomain, and so is their composition.
The sequential composition of the two interpretations is then
interpretation SET-TO-SEQ : SET => SEQ is
mediator SET-AS-BAG-AS-SEQ
dom-to-med SET-TO-SEQ
cod-to-med {}
5.4 Parallel Composition of Interpretations
Just as a specification can be put together from smaller specifications, so can an interpretation (refinement) of a specification be put together from interpretations on component specifications. In Specware, the primary method for combining specifications is the colimit operation. If we have interpretations for each of the specifications in a given diagram, we may compose them to obtain an interpretation whose domain is their colimit. The codomain of the composed interpretation will be the colimit of another diagram. The nodes of this second diagram are labeled with the codomains of the component specifications.
In addition to refining its component specifications, we can also change the shape of the given diagram itself. For example, we might begin with a diagram with three morphisms between four specifications and end with a diagram with two morphisms between three specifications. This could happen because we may need to identify components that are distinct in the given diagram of specifications. Thus, to perform a parallel composition we have to say how the shape of the given diagram of specifications is to change.
A parallel composition is illustrated in Figure 13.
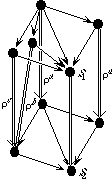
Figure 13: A Parallel Composition
On the top level, S1 is the colimit of a diagram of four specifications; on the bottom level, S2 is the colimit of a diagram of three specifications. The interpretations rra through rrd are interpretations that map the components of the top diagram into the components of the bottom diagram. The interpretation rr is the parallel composition of the four component interpretations; it maps the colimit S1 of the top diagram into the colimit S2 of the bottom diagram.
Not all interpretations on the specifications of a diagram can be composed; for the parallel composition to be applied, it is necessary for the interpretations to satisfy a compatibility condition, which will be discussed later.
5.4.1 Interpretation Schemes
For parallel composition, it is necessary to introduce a generalization of an interpretation called an interpretation scheme (ip-scheme). An interpretation scheme has the same structure as an interpretation, but the target morphism can be an arbitrary morphism; it need not be a definitional extension.
Note that for an arbitrary source specification S and target specification T, there is an interpretation scheme from S to T, whose mediator is the colimit of S and T; the source and target morphisms are simply the cocone morphisms. This is not an interpretation because the target morphism is not necessarily a definitional extension; in fact, in general no interpretation from S into T exists. In other words, the notion of interpretation scheme is quite a bit looser than that of interpretation.
Let us see an example of an interpretation scheme.
Example 5.8 Interpretation Scheme.
The following is an interpretation scheme from the simple specification ONE-SORT into itself. Its mediator is a specification TWO-SORT-QUOTIENT with two sorts, one a quotient of the other, as follows:
spec TWO-SORT-QUOTIENT is
sorts B, Q
op r? : B, B -> Boolean
sort-axiom Q = B / r?
end-spec
In other words, r? is an undefined binary relation on B, and Q is the quotient of B modulo r?. The specification does not restrict the meaning of the sorts B and Q and the operation r? except to assert the quotient relationship in the sort axiom.
The interpretation scheme is then
interpretation ONE-SORT-VIA-QUOTIENT :
ONE-SORT => ONE-SORT is
mediator TWO-SORT-QUOTIENT
dom-to-med {X -> Q}
cod-to-med {X -> B}
In other words, in this interpretation scheme, the sort X in the domain specification ONE-SORT is identified with the quotient, modulo r?, of the sort X in the codomain specification ONE-SORT.
Note that, because the relation r?, which is outside the image of the target morphism {X->B}, is not defined, the target morphism is not a definitional extension, and the interpretation scheme is not an interpretation.
5.4.2 Interpretation Morphisms
Up to now, we have applied the colimit operation only to specifications. To define the parallel composition of interpretations, we must employ a colimit of interpretations instead.
When we wanted to construct a colimit of specifications, we discussed first morphisms between specifications and then diagrams whose nodes are specifications and whose arcs are morphisms between them. Similarly, to construct a colimit of interpretations, we introduce first morphisms between interpretations and then diagrams whose nodes are interpretations and whose arcs are morphisms between them. The morphisms tell us which parts of the interpretations are to be identified. In this way, we extend to interpretations ideas we have already seen for specifications. We will also be able to take the colimit of a mixture of interpretations and interpretation schemes; the result will be an interpretation scheme but not necessarily an interpretation.
Definition 5.9: Interpretation Morphism.
An interpretation morphism from an interpretation rr1 : S1 => T1 to another interpretation rr2 : S2 => T2 is a triple of specification morphisms such that the diagram on the right below commutes. 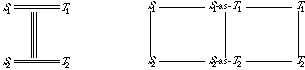
In other words, any specification element will be mapped into the same element regardless of which path through the diagram we choose.
The figure on the left is a summary of the one on the right. Note that the interpretation morphism is indicated by a triple arrow. As usual, specification morphisms and interpretations are indicated by single and double arrows, respectively.
It is possible that the source or target is an interpretation scheme rather than an interpretation; then the morphism is an interpretation-scheme morphism rather than an interpretation morphism.
Like a specification morphism, an interpretation morphism indicates how its source can be regarded as a part of its target--but in this case its source and target are both interpretations, not specifications.
Figure 14: An Interpretation Morphism
Example 5.10 Interpretation-Scheme Morphism.
Figure 14 illustrates an interpretation-scheme morphism, called ONE-SORT-SEQ-QUOTIENT. The target of this morphism in the interpretation BAG-TO-SEQ, from bags to sequences, that we have seen in Section 5.3, page 72. The source of this morphism is the interpretation scheme ONE-SORT-VIA-QUOTIENT, from ONE-SORT into itself, that we saw in the preceding section. The top part of the figure shows some of the details of the morphism--the bottom part is a summary.
Note that the diagram for the interpretation-scheme morphism commutes, as it must. For a morphism to exist between two interpretations or ip-schemes, they must be in a certain sense analogous. Each morphism between specifications at the source (upper) level is mapped into an appropriate morphism at the target (lower) level.
For instance, in the source interpretation scheme, X in ONE-SORT gets mapped into the quotient sort Q in TWO-SORT-QUOTIENT, just as, in the target interpretation, Bag in BAG gets mapped into the quotient sort Bag-as-Seq in BAG-AS-SEQ. The morphism {X -> Q} from ONE-SORT into TWO-SORT-QUOTIENT at the source level is mapped into the morphism that included the replacement Bag -> Bag-as-Seq from BAG into BAG-AS-SEQ at the target level. This is as it must be, because the interpretation-scheme morphism maps the sort X in ONE-SORT into the sort Bag in BAG, and the sort Q into the sort Bag-as-Seq. Otherwise the diagram would not commute.
Often, in presenting an interpretation morphism, we shall omit the details of how specification morphisms at the source level are mapped into specification morphisms at the target level, since it usually can be deduced from how the sorts are mapped.
Normally we construct and view an interpretation morphism through the graphical facilities of Specware. But the same morphism may be viewed textually.
ip-scheme-morphism ONE-SORT-SEQ-QUOTIENT :
ONE-SORT-VIA-QUOTIENT -> BAG-TO-SEQ is
domain-sm morphism ONE-SORT -> BAG is {X -> Bag}
mediator-sm morphism TWO-SORT-QUOTIENT -> BAG-AS-SEQ is
{(r?: B, B -> Boolean) -> (perm?: Seq, Seq -> Boolean),
Q -> Bag-as-Seq,
B -> Seq}
codomain-sm morphism ONE-SORT -> SEQ is {X -> Seq}
Incompatibility. It can be impossible to find an interpretation morphism between certain pairs of interpretations. For example, suppose in the preceding example we attempted to take our source interpretation to be the identity from ONE-SORT into itself, instead of the interpretation scheme ONE-SORT-VIA-QUOTIENT. We are attempting to find an interpretation morphism from the identity into the interpretation BAG-TO-SEQ. Figure 15 illustrates a partially filled-in interpretation morphism.
Figure 15: A Failed Interpretation Morphism
Note that we cannot map the middle copy of X (on top) into any of the sorts of BAG-AS-SEQ (on the bottom) and obtain a commuting diagram. If we map it into Seq, the left square does not commute; if we map it into Bag-as-Seq, the right square does not commute. The nonexistence of certain interpretation morphisms is related to the issue of compatibility in parallel composition of interpretations, as we shall see.
5.4.3 Categories
In developing the notion of an interpretation morphism, we have lifted the concept of a morphism from the category of specifications and applied it to another category of objects, that of interpretations. In fact, the notion of category can be given a precise mathematical meaning, so that concepts that are introduced for an abstract category can be immediately applied to specific instances of that category.
Definition 5.11: Category.
A category is an abstract mathematical structure with several components:
arrows f and g with the configurations 
we have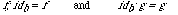
Let us give some examples of categories.
Example 5.12 The prototypical example of a category is the one whose objects are sets and whose arrows are functions from one set into another. The composition operation is simply the composition of functions; the identity arrow on a set is the identity function on that set.
To be precise, the arrows are triples of three components: function, domain, and range. In particular, we distinguish between the various identity functions on different sets; we don't identify ida, the identity function on set a, with idb, the identity function on set b. We do not identify the arrow with the set of ordered pairs that make up the function; adding more elements to the range of a function results in a different arrow, even though the set of ordered pairs in the function remains the same.
Sets are so pervasive that it is easy to forget that there are categories in which the objects are not sets. One such is the category of shapes.
Example 5.13 In the category of shapes, the objects are dots and the arrows are actually arrows between the dots. Here is a shape:
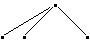
The composition of two arrows is an arrow with the following configuration

Here the long arrow is the composition of the two short arrows.
The identity arrow is an arrow from a dot to itself: 
Note that shapes are a multigraph; in other words, there may be more than one arrow between the same pair of dots. Of the several arrows between a dot and itself, one of them is designated as the identity for that dot.
Because objects in category theory are not necessarily sets, definitions in category theory must avoid relying on set properties of objects, although set-theoretic concepts do motivate some of the notions of category theory.
Example 5.14 In the category Spec, the objects are specifications and the arrows are specification morphisms. The composition operation is the composition of morphisms, and the identity arrow is the identity morphism.
Similarly, in the category Interp, the objects and arrows are interpretations and interpretation morphisms, respectively.
5.4.4 Interpretation Diagrams and Shape Mappings
Definition 5.15: Interpretation Diagram A diagram of interpretations is a graph, each of whose nodes is labeled with an interpretation and each of whose arcs is labeled with an interpretation morphism. To be well-formed, each arc must be labeled with an interpretation morphism whose source and target agree with the interpretations at the corresponding nodes. To be precise, the graph is really a directed multigraph--arcs are arrows and a pair of nodes may have more than one arc between them.
Because we must change shapes, we also introduce shape mappings, which change the shape of a diagram. To describe a shape mapping, first recall (Example 5.13) that a shape is a directed multigraph whose nodes are simply dots.
A shape mapping transforms a shape, e.g., by adding or deleting nodes or arrows or by identifying some of them. For example, one shape mapping might transform the left shape into the right shape as follows:
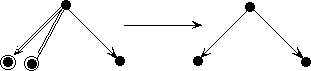
In this figure, the two ``selected'' nodes on the left, and the corresponding two selected arrows, have been merged to form the figure on the right.
A diagram of specifications can be viewed as a mapping that assigns a specification to each node of a shape and a morphism to each of its arrows. For example, consider a diagram d1 of four specifications:
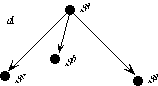
This can be viewed as the following mapping from a shape into the category Spec of specifications; we omit the morphisms:
Similarly, a diagram of interpretations can be viewed as a mapping from a shape into the category Interp of interpretations.
Parallel composition is applied to a diagram refinement, which combines a diagram of interpretations and a shape mapping. The diagram of interpretations provides the interpretations on the source components; the shape mapping allows us to identify and reconfigure target components.
Definition 5.16: Diagram Refinement. A diagram refinement <bb,ss> has two components:
The interpretation diagram dd : I1 -> Interp assigns an interpretation to each node of a shape I1 and an interpretation morphism to each of its arrows. The shape mapping ss maps the shape I1 into a shape I2. The definition requires that the following diagram commutes: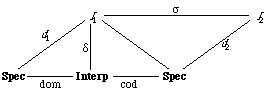
A diagram refinement can be regarded as an interpretation between diagrams of specifications. In the figure, d1 and d2 are two diagrams of specifications, which assign a specification from Spec to each of the nodes of the shapes I1 and I2, and a morphism to each of its arrows. Also, dom and cod map interpretations into their corresponding domains and codomains. The diagram refinement can be viewed as an interpretation whose domain is the diagram d1and whose codomain is the diagram d2.
Example 5.17 In the case in which I1 and I2 are shapes with four and three nodes, respectively, a diagram refinement can be illustrated like this:

Here d1 is a diagram of four specification, S1a through S1d, with shape I1. (We omit the morphisms between them.) For these specifications there are interpretations rra through rrd that map them into specifications S2a through S2d, respectively. As it turns out, the specifications S2b and S2c are the same.
The mapping dd is a diagram of the four interpretations rra through rrd --we omit the interpretation morphisms between them. The mapping ss is a shape mapping--it maps the shape of four nodes I1 into the shape of three nodes I2, collapsing the two nodes with the same specification. The pair <dd,ss> constitutes a diagram refinement.
The mapping d2 is a diagram of three specifications, S2a, S2b (= S2c), and S2c, with shape I2. The diagram refinement can be thought of as an interpretation from the diagram d1 into the diagram d2. Note that the composition ss ; d2 of the shape mapping ss with the diagram d2 can also be viewed as a diagram with shape I1, labeled with the four specifications S2a through S2d; we shall refer to this as the intermediate diagram. Thus hidden in the figure we actually have three specification diagrams, d1, ss ; d2, and d2, and a diagram of interpretations dd.
In the following definition, we invoke the notation of the definition of a diagram refinement.
Definition 5.18: Parallel (Horizontal) Composition of Interpretations.The parallel composition of the diagram refinement <dd,ss> is an interpretation from the colimit of the source diagram d1 into the colimit of the target diagram d2.
To compute the parallel composition, Specware first computes the colimit rr1of the diagram of interpretations dd. The colimit is itself an interpretation, whose source is the given colimit S1and whose target is the colimit S'2 of the intermediate diagram ss ; d2, which has shape I1. Note that this is not the desired colimit S2 of the target diagram d2, which has a different shape I2. The colimit construction, however, determines a morphism rr2, whose source is the colimit S'2 and whose target is the desired colimit S2. The composition rr1 ; rr2 of rr1 with rr2 is the parallel composition of the diagram refinement <dd,ss>. It has the property that the entire diagram commutes.
We shall denote the parallel composition of a diagram refinement DD by |DD||.
Figure 16: A Parallel Composition
Example 5.19 In Figure 16, we illustrate the parallel composition of the diagram refinement we looked at earlier in Example 5.17. Here we view the diagrams with the specifications placed directly on the nodes of the shape, not linked by arrows. The specifications S1, S'2, and S2 are colimits of the three specification diagrams d1, ss ; d2, and d2, respectively. The interpretation rr1 is the colimit of the diagram of interpretations dd. The morphism rr2, which maps S'2 into S2, is defined by the colimit construction. The parallel composition |<dd,ss>| is then the composition rr1 ; rr2.
Let us illustrate parallel composition with an example.
Example 5.20 Sequences of Sets.
Let us suppose we want to implement sequences of sets of elements of sort E, where E is finite; for instance, if E is the integers from 0 through 7, we would like to represent an object such as the sequence [{0, 7}, {1, 3, 6}].
Sequences of sets of sort E will be represented by arrays of bit vectors of size k. For instance, the sequence [{0, 7}, {1, 3, 6}] would be represented by the array
[[0, 1, 0, 1, 0, 0, 1, 0], [1, 0, 0, 0, 0, 0, 0, 1]]
Note that the order of the sets is reversed in the representation. Note also that our representation choices must be coordinated: the size of the array elements must agree with the size of the bit vectors. If the size of array elements is specified by a declaration, so is the size of the sets we can represent.
We begin with the colimit of a diagram that has specifications SEQ and SET glued together by the specification ONE-SORT to indicate that the elements of the sequences are to be identified with the sets.
Figure 17: Colimit for Sequences of Sets
This colimit is illustrated in Figure 17. Here is the corresponding text:
spec SEQ-OF-SET is
colimit of diagram
nodes ONE-SORT, SEQ, SET
arcs ONE-SORT -> SEQ : {X -> E},
ONE-SORT -> SET : {X -> Set}
end-diagram
We have already seen refinements of basic sequences into arrays (in Example 5.4, page 73), and finite sets into fixed bit vectors (in Example 5.5, page 75); now let us compose these interpretations so that the colimit, which specifies sequences of sets, will be interpreted accordingly as arrays of fixed bit vectors.
In practice, constructing a parallel composition of interpretations is done using the graphical facilities of Specware, rather than within the textual language, because the editing of three-dimensional graphs can be complex and is best done visually.
We shall refer to the notation of our general discussion of parallel refinement. Our given specification diagram d1, before taking the colimit, is:
The shape I1of this diagram is:
The diagram d1 assigns a specification to each node of the shape I1. It may be viewed as a mapping from I1to the category Spec of specifications. Each node of I1 is mapped into a specification and each arrow is mapped into a specification morphism. For instance, the left arrow is mapped into the morphism {X -> E} from ONE-SORT into SEQ.
A parallel composition applies to a diagram refinement, which has two components, a diagram of interpretations and a shape mapping. The diagram of interpretations, dd, assigns an interpretation to each node of the shape I1 and an interpretation morphism to each of its arrows. The domains of the interpretations are the three specifications in our given diagram d1, namely ONE-SORT, SEQ, and SET. The three interpretation assignments are as follows:
We have assigned an interpretation to each node of the shape I1; we must also assign an interpretation morphism to each of its two arrows. For instance, the interpretation morphism assigned to the first arrow maps the identity interpretation into SEQ-TO-ARRAY, and the interpretation morphism assigned to the second arrow maps the identity interpretation into SET-TO-BIT-VECTOR-FIXED. Some of the details of this diagram of interpretations are summarized as follows:
The top and bottom halves of the figure illustrate the interpretation morphisms assigned to the left and right arrows, respectively, of the shape I1. Note that the diagram commutes--if we could not find such interpretation morphisms, the parallel refinement would not be compatible. This figure reveals that the sort E of elements in the specification ARRAY is identified with the sort Bit-Vector-Fixed; this means that the target theory will describe arrays whose elements are bit vectors of fixed length.
The resulting interpretation diagram dd may be viewed as a morphism from I1 into the category Interp of interpretations. The final diagram d2 will have the same shape as d1. That is, I2 is identical to I1 and the shape mapping ss is the identity. The pair <dd,ss> is then a diagram refinement. To compute its parallel composition, Specware takes the colimit rr1 of the diagram of interpretations dd. Because the shape mapping in this case is the identity, this is also the desired parallel composition, an interpretation from the sequences-of-sets colimit into the arrays-of-bit-vectors colimit, illustrated as follows:
In this figure, the diagonal single arrows represent specification morphisms, the vertical double arrows represent interpretations. The parallel composition is the double arrow in the foreground.
Example 5.21 Sorting.
In the Sequences-of-Sets example the source and target colimit diagrams had the same shape; therefore we could take the shape mapping to be the identity. In this example, we find it advantageous to merge two of the nodes of the target diagram; therefore, we take a shape mapping ss different from the identity. We begin with a specification of the sorting problem.
Sorting. We suppose we want to specify a sorting function. The input will be a bag, the output will be a sequence, and the elements will be sorted according to a given transitive, total relation, called the sorting relation. The bag, sequence, and relation will all be defined over elements of the same sort. We shall require that the output have the same elements as the input, ordered according to the given relation. If an element occurs more than once in the input, it must occur the same number of times in the output. For example, if the input is {{4, 2, 4}} and the sorting relation is <=, the output should be [2, 4, 4]. Note that we do not specify the input to be a sequence, because the order in which the input elements appear is irrelevant.
The specification for sorting is given in Figure 18.
spec SORTING is
import colimit of
diagram
nodes ONE-SORT, BAG, SEQ, SORTING-RELATION
arcs ONE-SORT -> BAG : {X -> E},
ONE-SORT -> SEQ : {X -> E},
ONE-SORT -> SORTING-RELATION : {X -> E}
end-diagram
op ordered : Seq -> Boolean
op elements : Seq -> Bag
op sorted : Bag, Seq -> Boolean
definition of ordered is
axiom (ordered empty-seq)
axiom (ordered (prepend e empty-seq))
axiom (iff (ordered (prepend d (prepend e s)))
(and (rel-sort d e)
(ordered (prepend e s))))
end-definition
definition of elements is
axiom (equal (elements empty-seq) empty-bag)
axiom (equal (elements (prepend e s))
(insert-bag e (elements s)))
end-definition
definition of sorted is
axiom (iff (sorted b s)
(and (equal b (elements s))
(ordered s)))
end-definition
end-spec
Figure 18: Specification for Sorting
Note that the specification refers to another specification, SORTING-RELATION, given subsequently--this is the transitive, total relation. This and the specifications for bags and sequences are glued together by the specification ONE-SORT, to ensure that they are all defined over elements of the same sort, to yield a colimit S1. The three operations, ordered, elements, and sorted, are specified by definitions--thus the specification SORTING is a definitional extension of the colimit S1.
The predicate ordered determines whether a given sequence is in increasing order, according to the relation rel-sort, which is declared by the imported specification SORTING-RELATION. The axioms assert that any sequence of zero or one element is ordered. A longer sequence is ordered if its first two elements are in order, according to the relation rel-sort, and if the sequence of all but the first element is ordered. These axioms define the predicate ordered recursively.
The function elements yields the bag of elements of a given sequence. Finally, we define the predicate (sorted b s) to hold if the input bag b is the bag of the elements of the output sequence s and the output sequence is in increasing order.
The sorting relation rel-sort is specified to be a transitive, total relation, as follows:
spec SORTING-RELATION is
translate
colimit of
diagram
nodes
BINARY-RELATION, TRANSITIVE-RELATION, TOTAL-RELATION
arcs BINARY-RELATION -> TRANSITIVE-RELATION :
{br -> tr},
BINARY-RELATION -> TOTAL-RELATION :
{br -> tr}
end-diagram
by {tr -> rel-sort}
Note that, although sorting relations are typically required to be orderings, the reflexivity property is implied by totality and the antisymmetry property is not actually necessary.
The specification for transitive relations appears in Section 3.4, page 49. The specification for total relations is as follows:
spec TOTAL-RELATION is
import
translate BINARY-RELATION by
{br -> tr}
axiom total is
(or (tr x y)(tr y x))
end-spec
We shall not develop a sorting algorithm--we focus on the implementation of the data structures for the program. We shall use parallel refinement to implement the input bags themselves as sequences. If we took the shape mapping to be the identity, the target diagram would have two nodes labeled SEQ; this means that the target colimit theory would have two copies of the theory of sequences. This might be useful if we wanted to employ different representations for the input sequence (which represents a bag) and the output sequence. In subsequent refinements, we could implement these two sequences differently. It is wasteful, however, if we decide to use the same implementation for both sequences, because we would be constructing two copies of the same set of programs. Therefore, in this example we shall use a shape mapping that merges the two sequences into one.
Let us focus on the refinement of the diagram d1 from the sorting specification, before taking the colimit S1. This diagram is as follows:
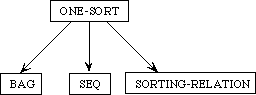
We may regard this diagram as a mapping from the shape I1 to the category Spec of specifications. We assign an interpretation to each node of I1. To the node labeled BAG in the diagram, we assign the interpretation BAG-TO-SEQ from bags into sequences. To the other nodes, we assign the identity interpretation. We also assign an appropriate interpretation morphism to each of the three arrows. The result is an interpretation diagram dd, a morphism from the shape I1 into the category Interp of interpretations.
To define a diagram refinement, we must also provide a shape mapping ss. Before we decide what ss should be, let us begin the construction of the parallel composition.
We first form the colimit rr1 of the diagram of interpretations dd. This is itself an interpretation. Its source is the colimit S1, which specifies bags, sequences, and a sorting relation over elements of the same sort. The target of rr1 is a specification of a theory that has two distinct versions of the theory of sequences, one to implement the input bags and the other to implement the output sequences. It is the colimit S'2 of an intermediate diagram with shape I1:
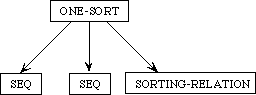
If we were to take ss to be the identity, rr1 would be our parallel composition and the colimit S'2 of the above diagram would be our target theory. Since we have decided to use the same implementation for the input and output sequences, we employ a shape mapping that merges the two nodes labeled SEQ. This is the shape mapping ss:
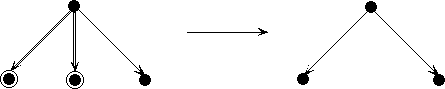
The left shape is I1 and the new right shape is I2. In this mapping, the two selected nodes of I1, and the corresponding two arrows, have been merged to form I2.
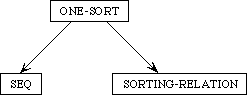
We are now ready to conclude constructing the parallel composition of the diagram refinement <dd,ss>. The theory we want is the colimit S2 of the corresponding diagram d2 with shape I2, illustrated as follows:
The colimit process allows us to define a morphism rr2, which maps S'2 into S2. When we compose rr1 with rr2, we obtain the parallel composition of the diagram refinement. The target of this parallel composition is the desired colimit S2. This is the intended target theory for the representation of bags, sequences, and sorting relations--it contains a single copy of the theory of sequences to serve as the implementation of both the input bag and the output sequence.
The entire parallel-composition construction is illustrated in Figure 19:
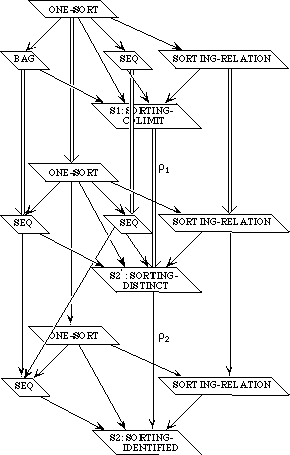
Figure 19: Sorting Refinement
We have obtained a parallel refinement of the colimit S1 from the sorting specification. Note that the sorting specification is not identical to the colimit--it is a definitional extension of that colimit. However if we construct a refinement of a specification, we can extend the refinement automatically to a definitional extension of that specification. That will be the subject of the next subsection. Afterwards, we shall discuss the sequential composition of parallel refinements.
5.5 Interpretation of Definitional Extensions
As we have remarked, if a specification S' is a definitional extension of a specification S, we can extend an interpretation of S automatically into an interpretation of S'. (This is not true of an arbitrary specification S' that imports S--an axiom of S' may be inconsistent with the interpretation.)
A graphical rendering of the extension of the interpretation is as follows: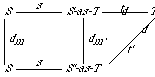
Here we have an interpretation of S into T and a definitional extension S' of S. The specification S'-as-T, constructed as a pushout of the morphisms s and m, is a definitional extension of S-as-T (because pushouts preserve definitional extension). We may think of S'-as-T as the extension of S-as-T obtained by introducing the images under s of the new definitions of S'. The morphism t' is the composition of t and m'. Because the target morphism t of an interpretation is a definitional extension, and because composition preserves definitional extension, t' is also a definitional extension. Hence t' is the target morphism and S'-as-T is the mediator of an interpretation from S' into T.
Example 5.22 Sorting, Continued.
In Example 5.21, we used parallel composition to obtain a refinement of part of the sorting specification, the colimit S1, into the new theory S2 of sequences and sorting relations over elements of the same sort. We remarked that the entire sorting specification is a definitional extension of the colimit, obtained by introducing definitions for the operations ordered, elements, and sorted. Therefore we may automatically extend our refinement to obtain a refinement from the entire sorting specification into the theory of sequences and sorting relations. In the general discussion, S and T play the role of S1 and S2, respectively, in the sorting example; S' corresponds to the sorting specification.
5.6 Composing Diagram Refinements
Often we want to follow one parallel refinement with another. Diagram refinements can be composed sequentially by composing the individual interpretations which they comprise. This is illustrated in the following figure:
Let <dd1, ss1>: d1 -> d2 and <dd2, ss2>: d2 -> d3 be two diagram refinements. We can juxtapose these as shown below: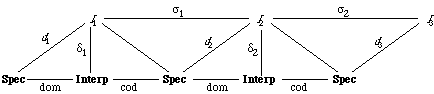
In this figure, we get two diagrams of interpretations with shape I1, namely dd1 and ss1 ; dd2, such that the codomains of the interpretations in the first diagram match the domains of the interpretations in the second diagram. By composing the individual interpretations sequentially, we get another interpretation diagram with shape I1. We will denote this horizontally composed diagram of interpretations by dd1o (ss1 ; dd2). The shape mapping for the composed diagram refinement is obtained by composing the individual shapemappings, ss1 ; ss2:I1 -> I2->I3. Thus, <dd1o (ss1 ; dd2), ss1 ; ss2> : d1 -> d3 is the composition of the two diagram refinements we started with. The composition is indicated in the following figure:
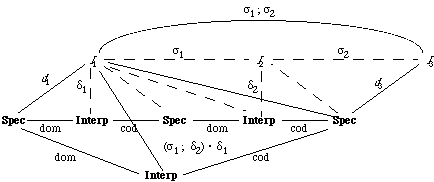
Thus the composition of two diagram refinements, indicated with dotted arrows, is also a diagram refinement, indicated with solid arrows.
The Interchangeability of Sequential and Parallel Composition. Sequential and parallel composition of interpretations satisfy the following interchange law: If DD1: d1 -> d2 and DD2: d2 -> d3are two diagram refinements which can be composed, then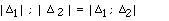
In other words, the result of computing the parallel compositions of the two diagrams separately and then composing the results sequentially is the same as the result of composing the many separate components sequentially and then computing the parallel composition of the resulting diagram.
The following example will illustrate the sequential composition of two parallel compositions and the interchange law. It will also bring up some compatibility issues.
Example 5.23 Bags of Bags.
In Example 5.20, we used parallel refinement to develop an implementation for sequences of sets, where the elements of the sets were of a finite sort E. In this example, we shall develop a refinement of a specification that describes bags whose elements are themselves bags of sort E, where E is not necessarily finite. We shall represent both sorts of bags as sequences; the target theory will be sequences of sequences. Unlike in the sorting refinement (Example 5.21), we shall be forced to have two copies of the sequence specification, not one, in the target theory.
In the previous examples, Sequences of Sets and Sorting, we were able to refine components in parallel because the refinements did not interfere with each other. For instance, the refinement of sets into fixed bit vectors did not collide with the refinement of sequences into arrays--sets and sequences were not identified in the colimit.
In this example, we start with two copies of the specification for bags, an ``outer'' copy and an ``inner'' copy. The two copies are not independent; the elements of the outer copy are identified via a colimit with the bags of the inner copy. For example, the bag {{ {{X, Y, Y}}, {{Y, Y, Z}} }} is a bag of the outer copy--its two elements are both bags of the inner copy.
To specify bags of bags, we form the following colimit:
spec BAG-OF-BAGS is
colimit of
diagram
nodes ONE-SORT, OUTER : BAG, INNER : BAG
arcs
ONE-SORT -> OUTER : {X -> E},
ONE-SORT -> INNER : {X -> Bag}
end-diagram
The diagram of this colimit is presented graphically as follows:
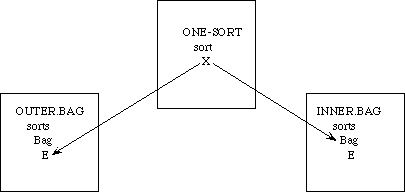
Note that the two copies of the bag specification are glued together by morphisms from the specification ONE-SORT. The sort X of that specification is mapped into the elements of the outer bag specification and the bags of the inner bag specification; that is, these three sorts are identified. In a parallel refinement, when any of them is mapped into another by an interpretation, the other two must be mapped in such a way as to avoid incompatibility. In this case, it turns out that we cannot perform these two refinements in parallel. Instead we perform the refinement in two stages, as a sequential composition of two parallel refinements. In a subsequent note, we explore what mishaps occur if we attempt to perform both refinements at the same stage.
Stage One: Inner Bags into Sequences. At the first stage of the refinement process, we refine the inner copy of BAG into SEQ, by applying the interpretation BAG-TO-SEQ we developed in Example 5.3, page 71. This refinement represents the bags by a quotient of sequences modulo the permutation relation; in other words, each bag is mapped into an equivalence class of several finite sequences, all of them permutations of each other.
We refine the specification ONE-SORT to itself by applying the interpretation scheme ONE-SORT-VIA-QUOTIENT we introduced in Example 5.10, (Interpretation Morphism), page 86. This ip-scheme maps a sort into the quotient of a sort modulo an equivalence relation.
To maintain compatibility, our refinement of the outer copy of BAG must be analogous; otherwise we couldn't construct an interpretation-scheme morphism into the refinement from ONE-SORT-VIA-QUOTIENT. We therefore represent the bag elements as the quotient of other elements modulo some relation. For this purpose, we introduce a specification that describes two sorts of bags B.Bag and Q.Bag, over elements of sort B and Q respectively, where Q is a quotient sort of B. The specification BAG-QUOTIENT, which appears in part as follows, will serve as the mediator for the interpretation. The sort E of elements of the outer copy of bags will be mapped into the quotient sort Q in the mediator.
spec BAG-QUOTIENT is
import
translate
colimit of
diagram
nodes B : BAG, Q : BAG
end-diagram
by {B.E -> B,
Q.E -> Q}
op r? : B, B -> Boolean
sort-axiom Q = B/r?
<axioms omitted>
end-spec
The axioms, which we omit here, define the Q-operations in terms of the B-operations. This specification is discussed in the next subsection and appears in full in the appendix (Section G, page 168).
The interpretation scheme that maps bags into bags via the quotient sort is as follows:
interpretation BAG-VIA-QUOTIENT : BAG => BAG is
mediator BAG-QUOTIENT
dom-to-med BAG-TO-Q-BAG
cod-to-med BAG-TO-B-BAG
Here BAG-TO-Q-BAG and BAG-TO-B-BAG are morphisms that map the usual bag sorts and operations into those for bags of elements of sorts Q and B, respectively, in BAG-QUOTIENT. For example, the source morphism is
morphism BAG-TO-Q-BAG : BAG -> BAG-QUOTIENT is
{Bag -> Q.Bag,
E -> Q,
empty-bag -> Q.empty-bag,
insert-bag -> Q.insert-bag,
in-bag? -> Q.in-bag?}
The target morphism, BAG-TO-B-BAG, is analogous.
In the interpretation scheme BAG-VIA-QUOTIENT, the sort E of elements of the domain bags is mapped into the quotient sort Q in the mediator; the sort E of elements in the codomain bags is mapped into the sort B of basic elements in the mediator. Because the relation r? remains undefined, this is an interpretation scheme, not an interpretation.
We have defined three interpretations (including the interpretation scheme), which constitute the three nodes of a diagram of interpretations dd. The two arrows of the diagram correspond to two interpretation morphisms. One of these morphisms was presented in Example 5.10 (Interpretation Morphism), page 87; the other is analogous.
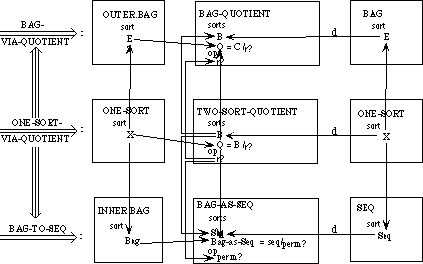
Figure 20: First Diagram of Interpretations for Bags of Bags
We may summarize this first diagram of interpretations in Figure 20. Here, single arrows indicate morphisms, double arrows indicate interpretations, and triple arrows indicate interpretation morphisms. The left part of the diagram, before the colons, gives a high-level view; the right part gives the details. We show only how the shared sorts are mapped.
Recall that the target morphisms of our interpretation schemes are not definitional extensions only because the relation r? is undefined in the mediators BAG-QUOTIENT and TWO-SORT-QUOTIENT. These relations are identified by morphisms with the relation perm? in the mediator BAG-AS-SEQ. Because this relation is defined, the target morphism of the parallel composition is a definitional extension. Thus the parallel composition will be an interpretation, even though two of its components are only interpretation schemes.
It may seem as if we are doing a lot of work for this particular refinement. However, the ip-schemes of bags into bags via the bag of quotients and of ONE-SORT-VIA-QUOTIENT are library refinements and are reused in any parallel refinement of this kind.
We do not change the shape of our diagram; the shape mapping ss is the identity. If we take the parallel composition of this diagram refinement, we obtain a new interpretation, from the first colimit, which specifies bags of bags, to a new colimit, which specifies bags of sequences. The parallel composition is illustrated in Figure 21.
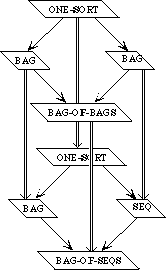
Figure 21: Stage One: Inner Bags into Sequences
In our next subsection, we give more details about the mediator for the refinement of bags into bags via the quotient; in a subsequent subsection, we continue with the parallel refinement of the specification BAG-OF-BAGS.
The mediator BAG-QUOTIENT. Although the mediator BAG-QUOTIENT in not a definitional extension of the codomain, because r? is undefined, all the sorts and operations of the Q-copy of the bag theory are defined in terms of the sorts and operations of the B-copy. In particular, the Q-bags are intuitively regarded as bags whose elements are equivalence classes of elements of sort B, modulo the equivalence relation r?. It is more convenient, however, to regard the Q-bags as equivalence classes of B-bags under a new equivalence relation eq-bag-mod-r?, called equality modulo r?. Two B-bags are equal modulo r? if we can establish a one-to-one correspondence between the elements of the two bags such that corresponding elements are equivalent under r?.
For example, consider the Q-bag intuitively regarded as {{ {B1, B2}, {B, B} }}. The elements of this bag are equivalence classes of elements of sort B modulo r?; thus B1 and B2 are equivalent under r?. The mediator will actually regard this as an equivalence class of two equivalent B-bags, {{B1, BB}}and {{B2, BB}}, modulo eq-bag-mod-r?.
All the operations on Q-bags are defined in terms of operations on B-bags. Thus, the mediator contains the following definition of Q.empty-bag in terms of B.empty-bag:
definition of Q.empty-bag is
axiom (equal Q.empty-bag ((quotient eq-bag-mod-r?) B.empty-bag))
end-definition
Note that the definition is expressed in terms of the quotient function modulo the new equivalence relation--that is the motivation for representing the Q-bags in this unintuitive way.
The mediator also contains definitions for the function Q.insert-bag and the predicate Q.in-bag?. These are given in the full specification of the mediator, on page 169. We now resume our discussion of the refinement of the specification for bags of bags.
Stage Two: Outer Bags into Sequences. In the simpler second stage of the refinement process, we refine the outer copy of BAG into SEQ, again by applying the interpretation BAG-TO-SEQ. This interpretation will represent the bags by a quotient, but will simply map the elements of the bags into the elements of the sequences. The corresponding sorts of elements (of ONE-SORT) and sequences (of the inner copy of SEQ) will be mapped into elements and sequences, respectively; we refine these nodes via the identity interpretations.
We can then map the identity interpretation on ONE-SORT into the other two interpretations, via two interpretation morphisms. The outer interpretation morphism maps the sort X (in the domain, mediator, and codomain copies of ONE-SORT) into the sort E; the inner interpretation morphism maps the sort
X into the sort Seq each time. This gives us our second diagram of interpretations dd which is summarized in Figure 22.
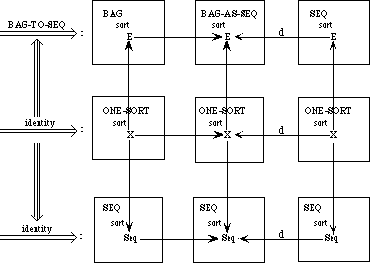
Figure 22: Second Diagram of Interpretations for Bags of Bags
If we attempted to identify our two copies of sequences, as we did in the refinement of sorting, we would obtain a theory in which the elements of the inner sequences were identified with the sequences themselves. This is not inconsistent but it isn't what we intend; we might want the elements to be of another sort, such as the nonnegative integers. Instead we take the shape mapping ss to be the identity, and obtain a theory with two copies of the theory of sequences.
The parallel composition of the diagram refinement <dd, ss> composed with the parallel refinement from the first stage is illustrated in Figure 23.
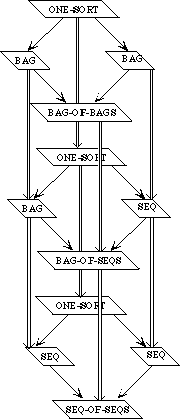
Figure 23: Refinement of Bags of Bags
Incompatibility. The example Bags of Bags allows us to illustrate how incompatibilities might arise in building a parallel composition of refinements. Suppose we attempted to refine both copies of bags into sequences at the same stage. When we refine the outer copy of the bags, the elements are represented by the elements of the outer copy of the sequences in the target. When we refine the inner copy of the bags, the bags are represented as a quotient of sequences modulo the permutation relation. But in the source, the elements of the outer bags are identified with the inner bags; in the target, the elements of the outer sequences are identified with the inner sequences. If all these sorts are to be identified, the sequences will be identified with the quotient of the sequences modulo the permutation relation, which would violate the freeness restriction (page 17).
More precisely, our problem is one of filling in the missing pieces of the diagram in Figure 24.
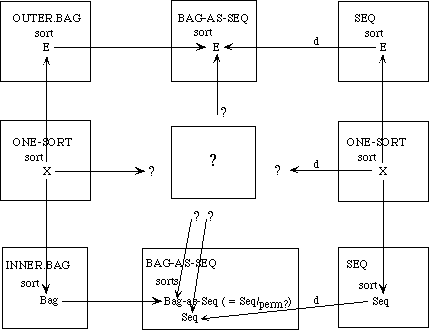
Figure 24: Incompatibility
`
However we fill in the mystery specification ?,we can see by following arrows around the diagram that two sorts in the inner mediator, Bag-as-Seq and Seq, will be identified, even though one is a quotient of the other, violating freeness.
Example 5.24 Bags of Bags, Continued.
In the example Bags of Bags, we formed a diagram of three interpretations and constructed their parallel composition. We then formed a diagram of three subsequent interpretations and again constructed their parallel composition. Finally, we took the sequential composition of the two resulting interpretations.
According to the interchange law, we could instead have separately composed the three interpretations from the first stage with the corresponding three interpretations, respectively, from the second stage. Then we could have taken the parallel composition of the three resulting interpretations. The final refinement would have been the same. We illustrate this process in Figure 25.
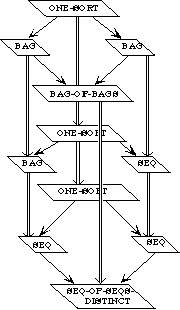
Figure 25: Alternative Refinement of Bags of Bag
6 Code Generation
When specifications are sufficiently refined, we may use them to generate programs that satisfy them. The programs will have implementations, in a desired target language, for all the operations in the given specification.
Roughly speaking, this is done by constructing interpretations into theories that describe the target programming languages, such as Lisp, C, or Ada. However, there are differences between the logic of specifications and the logics of programming languages; the notion of entailment, which describes logical deduction, may be different. For example, while our specification logic is strongly typed and all operations are completely defined on their types, the language Lisp is not strongly typed and functions may not be defined and may not terminate for some legal inputs. For this reason, generating programs requires some loosening of the notion of a specification and an interpretation to encompass multiple logics.
We describe target languages not only with Specware specifications but also with entailment systems, which are like specifications but which may employ a different logic. Rather than constructing an ordinary interpretation into an entailment system, we construct an entailment-system morphism (or es-morphism), a mapping that preserves logical entailment even though the source logic is different from the target logic. Such a mapping will map theorems into theorems though the notion of theorem-hood may be different. If we ignore some details, we can think of an es-morphism as a kind of interpretation. For a more exact description of entailment systems, see Meseguer's paper General Logics [Meseguer 89].The language of Specware is Slang; for each target programming language, there is a sublogic of Slang, called an abstract target language, that describes the constructs of the target language. For instance, there is an abstract target language SlangLisp that describes the constructs of Lisp.
The abstract target language is still a subset of Slang and employs Specware logic and syntax. For each target language, there is also an entailment system that describes the language in its own logic and syntax. For instance, in the entailment system EsLisp, which describes the language Lisp, operations are untyped. Sentences are function definitions, of the form
defun f (x)
(cond ((p x) (g x))
...))
and conditional equations, of the form
if (p x) (equal (f x) (g x))).
The entailment relation is one appropriate for reasoning about equations. Definitions in EsLisp are directly executable as programs.
There is a built-in entailment-system morphism from SlangLisp to EsLisp. Therefore, to translate the operations of any Specware specification into Lisp code, it suffices to build an interpretation from that specification into SlangLisp; that interpretation can then be composed with the built-in es-morphism. To translate into another target language, we construct an interpretation into another abstract target language, for which there exists an es-morphism into an appropriate entailment system.
6.1 Restrictions on the Abstract Target Language
We probably will not find the built-in abstract target language sufficient to represent all the operations in our specification; for instance, the abstract target language SlangLisp contains realizations only for integers and lists. When we build an interpretation into the abstract target language, however, we have a morphism into a definitional extension of that language; that is, we have enlarged the language with new definitions. Also, we may use the Specware specification-building operations explicitly to enlarge the abstract target language. For the system to generate code, these extensions and enlargements must satisfy a number of restrictions.
Colimit Independence. For a colimit specification, each component must have an implementation independently of the others.
Colimit Uniqueness. Each element in any of the components of a colimit may be the image of at most one element of another component. (Otherwise, elements would have more than one implementation.) Therefore, morphisms must be injective; they cannot map two distinct elements into the same element. Also, we cannot include diagrams such as the following, in which f
is the image of both g and h; otherwise we would have two definitions for f.
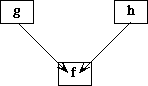
Constructiveness. Definitions must be constructive--that is, they must indicate a method of computing the corresponding operation. They may be either explicit, of the form
definition of f is
axiom (equal (f x) E)
end-definition
as in
(equal (square x) (times x x))
or conditional, of the form
definition of f is
axiom (implies (P1 x)
(equal (f x) E1))
axiom (implies (P2 x)
(equal (f x) E2))
end-definition
The antecedent conditions(P1 x)and(P2 x)must cover all possibilities; if both conditions hold, the values of E1 and E2 must agree. Of course the operation f may have more than one argument, or none, or it may be a constant. There may be more than two clauses in the definition and it may be recursive--occurrences of f may occur in E1 or E2. For a boolean operation f we may use iff instead of equal.
Note that, in the abstract target language, the operation f must be applied directly to variable arguments, not constants or complex terms. Thus the following definition for the length function, which is legal in Slang, is not constructive and is not allowed in SlangLisp:
definition of length is
axiom (equal (length nil) 0)
axiom (equal (length (cons x l))
((relax nonzero?)(succ (length l))))
end-definition
Here the arguments of length are a constant and a term, not variables. Definitions of this style in Slang specifications must be mapped by the interpretation into constructive definitions if we are to generate code from them.
We must rephrase definitions in terms of the ``destructors'', such as head and tail or pred, rather than the ``constructors'', such as nil and cons or succ.
No other operation may surround the operation f being defined. For example, a constructive definition for a function ncons may not contain the axiom
axiom (equal (head (ncons x)) x)
because a function symbol head surrounds the function ncons being defined.
An exception to these rules is that the built-in operations relax, quotient, and embed may surround the arguments or the defined function symbol in the definition. Special mechanisms in the es-morphism can translate such definitions into code. For example, in refining sets into bags, we have represented sets as a subsort of bags, those without duplicated elements. In the specification SET-AS-BAG, we define the sort Set-as-Bag by
sort-axiom Set-as-Bag = Bag | no-dup-bag?
We then have the following definition for the representation empty-s-as-b of the empty set:
definition of empty-s-as-b is
axiom (equal ((relax no-dup-bag?) empty-s-as-b) empty-bag)
end-definition
In other words, the empty set in the subsort is represented by the empty bag in the supersort. This is regarded as a constructive definition even though the defined constant empty-s-as-b is surrounded by a relax function.
Similarly, in refining bags into sequences, we have represented bags as the quotient of sequences modulo the permutation relation. In the specification for BAG-AS-SEQ, we have the following definition for the function insert-b-as-s, which represents the bag insertion function:
definition of insert-b-as-s is
axiom (equal (insert-b-as-s e ((quotient perm?) s))
((quotient perm?)
((relax nonempty?) (prepend e s))))
end-definition
In other words, the insertion function for bags is represented by the prepend function on sequences. This is regarded as a constructive definition even though argument s of the defined function insert-b-as-s is surrounded by a quotient function.
We have said that when a constructive definition is expressed as a set of implications, the antecedent conditions of the implications must cover all possibilities. This rule takes into account the following convention: a definition on a subsort is thought of as an implicit implication, with the condition that defines the subsort as its antecedent.
For example, the following is regarded as a constructive definition of the length function.
definition of length is
axiom (implies (null? nl)
(equal (length nl) zero))
axiom (equal (length ((relax nonnull?) nnl))
((relax nonzero?)(succ (length (tail nnl)))))
end-definition
The second axiom is thought of as an implication like the first, with the invisible, redundant antecedent (nonnull? ((relax nonnull?) nnl). Hence the antecedent conditions do cover all possibilities, if we consider the invisible ones. (Note that nl and nnl are variables, with implicit universal (fa) quantification.)
Living with these restrictions forces us to revise some of our specifications. For example, our original specification for sequences had a sort Seq of sequences but no separate sort of nonempty sequences. However, because we cannot give constructive definitions in terms of the constructors empty-seq and prepend, we must introduce destructors first-seq and rest-seq for sequences, to yield the first element of a nonempty sequence and the sequence of all the rest of the elements, respectively. Because the functions are not defined on the empty sequence, we introduce a sort NE-Seq of nonempty sequences and declare
op first-seq : NE-Seq -> E
op rest-seq : NE-Seq -> Seq
These operations will be mapped by an interpretation into the corresponding SlangLisp operations head and tail. The function prepend will now yield a nonempty sequence, not a sequence. (This explains why, in the definition for insert-b-as-s, the occurrence of (prepend e s) is surrounded by the operator (relax nonempty?)).
Sort Restrictions. Various restrictions may apply to the sort mechanism in the abstract target language. For instance, in SlangLisp, the only sort constructors allowed are -> and the product sort. A product sort cannot be the codomain of any operation.
In the refinement process, we map our given specification, which probably does not satisfy the preceding restrictions, into a definitional extension of the abstract target language that does. Although the definition of an operation in the source specification need not itself be constructive, to generate code for it we must map it into a definition that is constructive and expressed in terms of operations from the abstract target language.
6.2 The Entailment-System Morphism
The built-in es-morphism translates Slang constructs from the abstract target language into the corresponding programming-language constructs. For example, here is the SlangLisp definition for absolute value:
spec SLANG-ABS is
import INTEGER
op abs : Int -> Int
definition of abs is
axiom (implies (ge x zero)
(equal (abs x) x))
axiom (implies (lt x zero)
(equal (abs x) (minus zero x)))
end-definition
end-spec
The es-morphism from SlangLisp to EsLisp translates it into the corresponding EsLisp version:
spec ES-ABS is
import SLANG-BASE
op abs
(defun abs (x)
(cond ((>= x 0) x)
((< x 0) (- 0 x))))
end-spec
Note that the SlangLisp version of the definition of abs consists of a set of complementary axioms; the EsLisp version consists of a single conditional equation--sets of complementary axioms are not legal in EsLisp, while conditional equations are not legal in Slang. Also note that the SlangLisp version imports the specification for integers. The EsLisp version does not include definitions for integer operations, because these operations are built-in Lisp primitives. It does, however, import a specification SLANG-BASE, which defines logical operations that are in Specware but are not primitive in Lisp. The specification SLANG-BASE is as follows:
spec SLANG-BASE is
ops implies, iff
(defun implies (x y)
(or (not x) y))
(defun iff (x y)
(or (and x y)
(and (not x) (not y))))
end-spec
6.2.1 The Specifications LIST-PRIM, INTEGER, and LIST
The following specification in the abstract target language SlangLisp describes lists of elements of sort List-Elem.
Spec LIST-PRIM is
Sorts List-Elem, List
op nil : List
op null? : List -> Boolean
op cons : List-Elem, List -> List
op head : List -> List-Elem
op tail : List -> List
constructors {nil, cons} construct List
<axioms for primitives omitted>
end-spec
This specification describes a small fragment of Lisp. It does not describe Lisp atoms and it does not say what List-Elem is. Thus, although the es-morphism maps this specification into EsLisp, it does not have an independent implementation. It may be used as part of a diagram in which the meaning of List-Elem is specified; the colimit of the entire diagram may be specified using the ``instantiation'' mechanism, described subsequently, instead of the usual colimit mechanism.
The SlangLisp specification INTEGER, in contrast to our specifications NAT-BASIC and Nat, describes both nonnegative and negative integers.
Spec INTEGER is
Sort Integer
op less-than : Integer, Integer -> Boolean
op greater-than : Integer, Integer -> Boolean
op less-than-or-equal : Integer, Integer -> Boolean
op greater-than-or-equal : Integer, Integer -> Boolean
op iplus : Integer, Integer -> Integer
op minus : Integer, Integer -> Integer
op times : Integer, Integer -> Integer
op min : Integer, Integer -> Integer
op max : Integer, Integer -> Integer
constructors {zero, one, iplus, minus} construct integer
%% axioms omitted
end-spec
The axioms provide constructive definitions of these elements. In addition, there are declared the constants one, two, ..., ten, which denote the integers 1 through 10. There is an es-morphsim from this theory into EsLisp. Therefore, if we can refine a theory constructively into INTEGER, we can compose that interpretation with the es-morphism to generate LISP code for the theory.
There is a specification for a larger theory LIST, which imports both LIST-PRIM and INTEGER, that constructively defines additional Lisp functions, such as concat (the append function), sublist, and remove. Since this theory is a definitional extension of LIST-PRIM and INTEGER, if we can refine a theory constructively into LIST, we can generate Lisp code for the theory.
We may develop other constructive definitional extensions of LIST-PRIM and INTEGER. We can then create LISP code for a theory if we can refine it constructively into the extension.
6.2.2 Translating Constructed Sorts
There are numerous details in es-morphisms such as that from SlangLisp to EsLisp. We shall briefly consider the translation of constructed sorts.
Each element of a subsort is represented by the corresponding element of the supersort. For example, the element empty-s-as-b in the subsort of bags with no duplicated elements is represented by the bag((relax no-dup-bag?) empty-s-as-b) in the supersort of bags. (As we have seen, this is defined to be equal to the empty bag.) Similarly, quotient sorts can be handled by representing an equivalence class by one of its elements. For example, the bag {{4,2,4}} might be represented by the sequence [2,4,4].
Sentences are translated consistently with these representations. For example, the functions (relax p?) and (quotient r?), associated with the subsorts and quotient sorts respectively, are dropped. For functions that are defined on a subsort, however, an explicit runtime check on the argument is inserted into the code; if the argument does not satisfy the predicate p?, an error message is produced. For instance, before applying a function to a set represented as a bag with no duplicated elements, the implemented code would ensure that no-dup-bag? was true of the bag. Also, the equality on a quotient sort E/r? is replaced by the equivalence relation r? that defines the quotient sort; thus the equality relation on bags will be replaced by the permutation relation on sequences; for example, two bags represented by the sequences [2,4,4] and [4,4,2] would be judged to be equal.
Coproduct sorts are translated into covariant records. For example, consider the following fragment of a SlangLisp specification for a stack--the size of a stack is the number of items it contains:
sort-axiom Stack = E-Stack + NE-Stack
...
op size : Stack -> Int
definition of size is
axiom (equal (size ((embed 1) es))
zero)
axiom (equal (size ((embed 2) nes)) (
succ (size (pop nes))))
end-definition
This fragment is translated into the following piece of EsLisp:
op size, E-Stack?, NE-Stack?
(defun E-Stack? (s)
(= (car s) 1))
(defun NE-Stack? (s)
(= (car s) 2))
...
(defun size (s)
(cond
((E-Stack? s) 0)
((NE-Stack? s)
(1+ (size (pop (cdr s)))))))
Thus the empty stack is represented by a list whose car is 1, a nonempty stack by a list whose car is 2.
This translation exploits the generality of entailment-system morphisms. Note, for instance, that the sorts E-stack and NE-stack, that is, empty stack and nonempty stack, in the SlangLisp version, are translated into functions E-Stack? and NE-Stack? in EsLisp. This would be impossible for an ordinary refinement, in which sorts can only be mapped into sorts, not functions.
6.2.3 Translating Colimits
For suitable entailment-system morphisms, such as that from SlangLisp to EsLisp, we obtain a recursive procedure for code generation; code for the colimit is obtained by combining the code for its component specifications. Thus, if we can constructively refine each component of a diagram into a specification for which we have a realization in the target language, we can obtain a realization for the colimit of the diagram.
6.2.4 Translation by Instantiation
A special mechanism exists for translating diagrams of the following form:
Here we assume that some es-morphism exists from FOO into EsLisp. Recall that no translation exists from LIST-PRIM into EsLisp; this is because we need a separate specification to describe the elements of the lists in LIST-PRIM. However, the entire configuration can be translated into EsLisp by the instantiation mechanism. The lists of LIST-PRIM will be translated into Lisp lists, and the elements of the list will be translated into the same Lisp objects as the elements of sort E from the specification FOO.
6.3 Refinement for Code Generation
Although the following example illustrates many aspects of refinement that we have seen before, we use it to emphasize that special requirements are imposed on a refinement if we wish to use it to generate code.
Example 6.1 Sets of Nonnegative Integers.
We assume we want to generate Lisp code for a specification for sets of nonnegative integers. As we have already seen, we can implement sets in terms of bags and, in turn, implement bags in terms of sequences. Sequences can then be implemented as lists, which exist in the abstract target language for Lisp. Furthermore, we can implement nonnegative integers in terms of Lisp integers--they are the subsort of the integers satisfying the nonnegative predicate. That is the basis for the proposed implementation. We give highlights of the refinement here.
The specification for sets of nonnegative integers is as follows:
spec SET-OF-NAT-BASIC is
colimit of diagram
nodes ONE-SORT, SET, NAT-BASIC
arcs ONE-SORT -> SET : {X -> E},
ONE-SORT -> NAT-BASIC : {X -> Nat}
end-diagram
Here is a graphical presentation of the diagram for the colimit in the specification:
The specification SET is given in Section 3.3, page 45. The specification NAT-BASIC is the basic specification for the nonnegative integers given in Figure 1, in Section 1, page 4.
We employ a sequential composition of parallel refinements; thus at each stage we refine SET, ONE-SORT, and NAT-BASIC separately.
Stage One: Sets into Bags. At the first stage, we refine sets into bags. For this refinement, we have previously (in Example 5.2, page 68) introduced a mediator SET-AS-BAG, in which sets are regarded as a subsort of bags, those with no duplicated elements; thus the set {2,4} is represented by the bag {{2,4}}, and no set is represented by the bag {{2, 2, 4}}. To define the appropriate subsort of the bags, we defined in the mediator a predicate no-dup-bag?, which holds if a bag has no duplicated elements; we could then define the subsort Set-as-Bag by
sort-axiom Set-as-Bag = Bag | no-dup-bag?
Because we were not concerned with code generation, the definition of no-dup-bag? did not have to be constructive.
Now that we are considering code generation, we must be more careful. In generating a function defined on sets, the system will insert a runtime check to ensure that the bag that represents it satisfies the no-dup-bag? predicate. Therefore, the definition of no-dup-bag? must either be constructive itself or be mapped under refinement into a constructive definition.
We cannot formulate a constructive definition of no-dup-bag? because, in our theory, bags have no ``deconstructors'' analogous to head and tail in Lisp. We cannot map the definition of no-dup-bag? into a constructive definition because it occurs in the mediator SET-AS-BAG, not in the specification BAG, and is not influenced by the refinement process.
To get around this problem, we move the definition of no-dup-bag? from the mediator into the specification BAG itself. The resulting specification is called BAG-EXTEND. The definition will then be mapped under refinement into the predicate no-dup-seq? in the specification SEQ-EXTEND, which is in turn mapped into the predicate no-dup-list? in the specification LIST-EXTEND, a definitional extension of LIST-PRIM. Only this last definition is constructive. LIST-EXTEND serves as the mediator of the interpretation from sequences into lists.
Also, in the previous refinement, we introduced an abbreviation in the mediator: to simplify the reading, the function (relax no-dup-bag?) was abbreviated as bag-of-s-as-b. However, as we indicated, in code generation the relax function is given special treatment. Many of our axioms using the abbreviation bag-of-s-as-b are not regarded as constructive, even though they are constructive when we replace them by the corresponding axiom that uses relax explicitly. Therefore, when we are concerned about code generation, we sometimes need to use the relax operation explicitly, instead of abbreviations such as bag-of-s-as-b.
Because we are doing a parallel refinement, we must make corresponding refinements to the other two components, ONE-SORT and NAT-BASIC; at this stage, we apply the identity interpretation to these specifications.
The resulting configuration is illustrated in Figure 26:
Figure 26: Stage One: Sets into Bags
Stage Two: Bags into Sequences. In the second stage of the refinement, we implement bags in terms of sequences as in Example 5.3, page 71; for code generation, however, we use a constructive mediator BAG-AS-SEQ-EXTEND instead of the original mediator BAG-AS-SEQ. Bags are regarded as a quotient sort, of sequences modulo the permutation relation. Each bag is mapped into an equivalence class of sequences; thus the bag {{2,4}} is mapped into the class of two sequences, [2,4] and [4,2]. According to the way quotient sorts are implemented, either of these sequences will stand for the bag. The equality relation on bags will be implemented as the permutation relation perm? on sequences. Therefore we must have a constructive definition for perm?.
The original definition we gave for perm? was as follows:
op perm? : Seq, Seq -> Boolean
definition of perm? is
axiom (iff (perm? s t)
(fa (e) (equal (count e s) (count e t))))
end-definition
This definition is not constructive: it contains a quantifier (fa (e) ...). To evaluate this quantifier and check if the counts are equal for all elements e of E would require an infinite computation if E is infinite; instead we replace it by a constructive definition, in which we test if the counts are equal only for those elements e that actually occur in s or in t:
definition of perm? is
axiom (iff (perm? s t)
(and (eqcount-seq? s s t)
(eqcount-seq? t s t)))
end-definition
Here (eqcount-seq? r s t) is defined constructively to hold if every element of the sequence r occurs equally often in s and t. This describes a finite computation because there are only a finite number of elements in r
At this second stage of the parallel refinement, as in the first, we apply the identity refinements to the other components of the diagram, ONE-SORT and NAT-BASIC. The resulting configuration is as given in Figure 27.
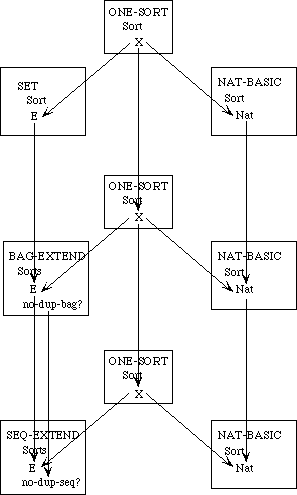
Figure 27: Sets into Sequences of Nonnegative Numbers
Stage Three: Nonnegative Integers into Integers. In the third stage, we refine NAT-BASIC, our specification for the nonnegative integers, into INTEGER, the SlangLisp specification for all the integers, including the negative integers, via a mediator NAT-BASIC-AS-INTEGER. In this refinement, the nonnegative integers are mapped into a subsort of the integers, those that satisfy the predicate nonnegative?. More precisely, the sort Nat in the nonnegative integers is mapped into the sort Nat-as-Int in the mediator, defined by
sort-axiom Nat-as-Int = Integer | nonnegative?
As in Bag of Bags (Example 5.23), to maintain compatibility we must perform analogous refinements on the other two components of the diagram, ONE-SORT and SEQ-EXTEND. This is because the three components share structure that is being altered by the refinement; because Nat is altered in NAT-BASIC, we must make corresponding alterations to X in ONE-SORT and E in SEQ-EXTEND; these three sorts are linked together by morphisms in the diagram.
The specification ONE-SORT is mapped into itself, not by the identity interpretation but via a mediator TWO-SORT-SUBSORT:
spec TWO-SORT-SUBSORT is
sorts Y, Z
op p? : Z -> Boolean
sort-axiom Y = Z | p?
end-spec
The sort X in ONE-SORT is mapped into the subsort Y in the mediator. An interpretation morphism (See Section 5.4.2) will map p? in this mediator into nonnegative? in the mediator NAT-BASIC-AS-INTEGER. The sorts Y and Z correspond to Nat and Integer respectively
The specification SEQ-EXTEND is also mapped into itself, via a mediator SEQ-EXTEND-SUBSORT, just as in refining bags of bags (Example 5.23, page 112) we mapped BAG into itself via a mediator BAG-QUOTIENT. The mediator imports the colimit of two copies of the sequence specification, over elements of sort C and D respectively. Sorts C and D are related in the mediator as follows:
op p? : D -> Boolean
sort-axiom C = D | p?
That is, C is the subsort of D containing those elements that satisfy p?.
The interpretation will map the domain sequences into the C-sequences (the sequences of elements of sort C in the mediator) and the codomain sequences into the D-sequences. The C-sequences are related to the D-sequences as follows:
sort-axiom C.Seq = D.Seq | all-p?
Here the predicate (all-p? ds) is defined (constructively) to hold if every element of a D-sequence ds satisfies the condition p?. Thus, if p? is the predicate nonnegative?, (all-p? ds) will hold if ds is the sequence [1,2,3] but not the sequence [-1,2,3]. The C-sequences are a subsort of the D-sequences--those whose elements all satisfy the condition p?.
Because we are interested in code generation, we must provide implementations for the sequence operations in the source specification SEQ-EXTEND in terms of the sequence operations in the target specification SEQ-EXTEND; this means that we must define the operations of the C--sequences constructively in terms of the operations of the D--sequences. For instance, we say
definition of C.empty-seq is
axiom (equal ((relax all-p?) C.empty-seq) D.empty-seq)
end-definition
Recall that (relax all-p?) maps a C--sequence into the same sequence regarded as a D--sequence. The definition then means that the empty C--sequence is the sequence that, regarded as a D--sequence, is the empty D--sequence. This is a constructive definition only because of the special treatment of the relax operator.
Because we have introduced functions first-seq and rest-seq into SEQ-EXTEND, we must relate the C--version of these functions with the corresponding D--versions. For example, we have
axiom (equal ((relax p?)
(C.first-seq cnes))
(D.first-seq
(d-of-c-ne-seq cnes)))
Here (d-of-c-ne-seq cnes) is a function defined in the mediator to map a nonempty C--sequence cnes into the same sequence viewed as a nonempty D--sequence.
This axiom corresponds to the following commutative figure:
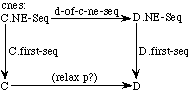
Figure 28 illustrates this stage of the refinement process, including the mediators.
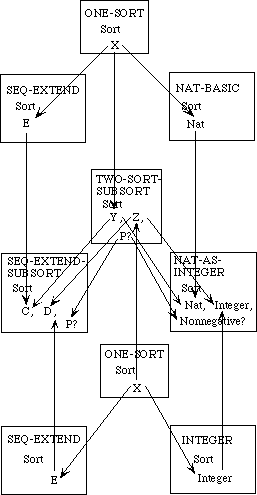
Figure 28: Third Stage: Nonnegative Integers to Integers
Stage Four: Sequences into Lists. In the fourth stage, we refine SEQ-EXTEND into LIST-PRIM, the SlangLisp specification for a fragment of Lisp. The interpretation is via a mediator LIST-EXTEND, which enriches LIST-PRIM with constructive definitions of operations, such as no-dup-list?, that are necessary for the representation of sets. In this representation, empty-seq is represented by nil, in-seq? by member, prepend by cons, and so forth.
At the same stage, we refine ONE-SORT into TRIV, which is actually identical to ONE-SORT except that TRIV is in SlangLisp and ONE-SORT is not. We also refine INTEGER into itself via the identity. These refinements can be performed in parallel, without causing incompatibilities. To see this, observe that the diagram in Figure 29 commutes--it illustrates just this last stage of the refinement process.
Figure 29: Stage Four: Sequences into Lists
Code Generation. We have constructed an interpretation from our initial specification for sets of nonnegative integers into a colimit of a diagram whose components are all SlangLisp specifications. Furthermore, all the operations of our initial specification have been mapped into constructive definitions based on SlangLisp primitives. Let us examine our final colimit diagram:

This diagram is of a form that can be translated by the instantiation mechanism. Therefore we can use the entire refinement to generate code for our original specification for sets of nonnegative integers. An es-morphism is constructed from SET-OF-NAT-BASIC into EsLisp. The target of this es-morphism, an EsLisp specification, will contain Lisp definitions that implement all the set operations of SET, as applied to elements that are nonnegative integers. It will also contain Lisp implementations of all the numerical operations in NAT-BASIC.
For instance, here is a sample of some of the generated code:
DEFUN INSERT-SET (X SB)
(IF (IN-BAG? X SB) SB
(IF (NOT (IN-BAG? X SB))
(INSERT-BAG X SB)
(CASE-ERROR))))
.
.
.
(DEFUN INSERT-BAG (E S)
(PREPEND E S))
Machine-generated function names have been simplified. Note that the programs implement, in Lisp syntax, the algorithms suggested by the appropriate constructive definitions from the specifications.
Part III Appendices
A Names
Specifications, morphisms and diagrams can each be named, as can many of their components, such as nodes and arcs of diagrams. There is a consistent syntax for introducing names, illustrated as follows:
NAMED NOT NAMED
spec <name> is spec
<development-element>* <development-element>*
end-spec end-spec
morphism m : <name> -> <name> { <sm-rules> }
is { <sm-rules> }
diagram <name> is diagram
<nodes-and-arcs> <nodes-and-arcs>
end-diagram end-diagram
The keyword is may be replaced by the symbol =.Names are used in the usual way to denote the objects to which they are bound. Thus, for example, in any syntactic context in which a specification is required, a name of a specification may be substituted.
A.1 Naming and Scoping Rules
Specifications, diagrams, and morphisms each have their own individual, global namespace. Thus the same name may be used to denote, say, a specification and a morphism. Because these namespaces are global, two different specifications (respectively, morphisms, diagrams) must have different names--there is no context that can disambiguate which specification a name refers to.
If a specification, diagram or morphism appears as a top-level expression, i.e., not as a subexpression of a diagram-, morphism- or specification-returning expression, it must be named. Otherwise, there is no way to refer to such an object.
On the other hand, a new name cannot be introduced in a lower-level subexpression. For example,
diagram FOO is
nodes X: spec Y is ... end-spec
end-diagram
is illegal since the specification at the lower-level node X cannot introduce the name Y.
The names of nodes and arcs are local to a diagram and have their own namespaces. This means that two diagrams may use the same name as a node name, and within the same diagram a node and an arc may have the same name.
Similarly the names used in a specification are local to the specification. Sorts, operations, definitions, and theorems all have distinct namespaces. It is not an error, however, for two operations to have the same name if type inference can be used to disambiguate references.
A.2 Lexical Conventions
Valid names start with either an upper- or lower-case letter or an asterisk (*), and are followed by any letter or digit or an asterisk (*), exclamation point (!), hyphen (-), or question mark (?). (Also, see Section B.2 in the BNF appendix.) Names are not case sensitive: all names are converted to uppercase internally.
The keywords in Slang are:
- arcs embed mediator-sm
- axiom end-definition morphism
- body-ip end-diagram nodes
- by end-spec of
- cocone-morphism ex op
- cod-to-med fa project
- codomain-sm from quotient
- codomain-to-mediator identity-morphism relax
- colimit import sort
- const import-morphism sort-axiom
- construct instantiate sorts
- constructors interpretation spec
- definition ip-scheme spec-interpretation
- diagram ip-scheme-morphism theorem
- dom-to-med is translate
- domain-sm lambda translation-morphism
- domain-to-mediator mediator
The following characters have special meaning depending upon the context:
( ) -> , | : = . < > { } [] / +
B Syntax
In this appendix, we define the syntax of Slang. Readers familiar with Refine may also wish to consult the file
<slang-top-level>/core4/code/language/spec-grammar.re.
B.1 Notation
To describe the syntax, we use BNF augmented with regular expression constructs. Non-terminals are enclosed in angle brackets, ``<...>''. Terminals are indicated by typewriter font. Syntax alternatives are separated by ``|''. Parentheses, ``(...)'', are used for grouping, e.g., for inline alternatives. Optional entities are enclosed in square brackets, ``[...]''. Writing a ``*'' after a syntactic element indicates zero or more repetitions of that element; a ``+'' indicates one or more repetitions.
B.2 Grammar
Top-Level Objects
The top-level objects of Slang are specifications, morphisms, and diagrams. Each such object class appears twice in the grammar, once with the prefix ``global-'' and once with the prefix ``local-''. Global objects must be named; local objects must not be named. Global objects can appear only at the top-level; local objects can appear only within other expressions.
<top-level-slang-object> ->
<global-spec> | <global-sm-diagram>
Specifications
<global-spec> ->
spec <symbol> (is | = >
[<import-declaration>]
<development-element>*
end-spec
|
spec <symbol>(is |=> <spec-operation>
Import Declarations
<import-declarationÒ Æ
import <spec-term> (,<spec-term>)* |
import <diagram-term>
Specification Elements
<development-element> ->
<sort-declaration> | <sort-axiom> \xbd <op-declaration> |
<constructor-set> | <theorem> | <definition>
<sort-declaration> -> (sorts | sort) <spec-sort> (, <spec-sort> )*
<spec-sort> -> <symbol>
<sort-axiom> -> sort-axiom <spec-sort-ref> = <spec-sort-term>
<op-declaration> -> (op | const) <symbol> : <spec-sort-term>
<constructor-set> ->
constructors { <spec-op-ref> (, <spec-op-ref>)*} construct <spec-sort-term>
<theorem> -> ( axiom | theorem) [ <symbol> ( is | =)] <spec-op-term>
<definition> ->
definition [ <symbol>[of <spec-op-ref>] ( is | = )]
<definition-clause> +
end-definition
<definition-clause> -> <theorem>
Sort Terms
<spec-sort-term> ->
<spec-sort-ref> | <spec-sort-function> | <spec-sort-subsort> |
<spec-sort-quotient> | <spec-sort-coproduct> | <spec-sort-product>
<spec-sort-ref> -> <qualified-name>
<spec-sort-function> -> [<spec-sort-term>] -> <spec-sort-term>
<spec-sort-subsort> -> <spec-sort-term> | <spec-op-term>
<spec-sort-quotient> -> <spec-sort-term> / <spec-op-term>
<spec-sort-coproduct> -> [ ] | <spec-sort-term> (+ <spec-sort-term>)+
<spec-sort-product> -> ( ) | <spec-sort-term> (, <spec-sort-term>)+
Precedence and Associativity for Sort Terms. The different operators for constructing sort terms are listed as follows in order of increasing precedence. Precedence can be overridden with parentheses.
precedence for <spec-sort-term>
brackets ( matching )
same-level -> associativity right
same-level ,+ associativity none
same-level |/
Terms and Formulas
<spec-op-term> ->
<spec-op-ref> | <spec-op-operation> | <spec-op-binding-operation> | <spec-op-product>
<spec-op-ref> -> <qualified-name> [ : <spec-sort-term>]
<spec-op-operation> ->
( <spec-op-term> <spec-op-term> * ) |
( ( project | embed ) <positive-integer> )
<spec-op-binding-operation> ->
( <spec-op-binding-rator> ( <bound-var * ) <spec-op-term> )
<spec-op-binding-rator> -> (fa | ex |lambda)
<bound-var> -> <symbol> [: <spec-sort-term>]
<spec-op-product> -> < <spec-op-term> * >
Specification Terms
Specification terms are terms that denote specifications. Generally terms are of three kinds: references to named objects, operations, and explicit terms for anonymous (or local) objects.
<spec-term> -> <spec-ref> | <local-spec> | <spec-operation>
<spec-ref> -> <symbol>
<local-spec> ->
spec
[<import-declaration>]
<development-element> *
end-spec
<spec-operation> -> <spec-translation> | <spec-colimit>
<spec-translation> -> translate <spec-term>by { [ <sm-rules>] }
<spec-colimit> -> colimit of <diagram-term>
Specification Morphisms
<global-signature-morphism> ->
morphism <symbol>: <spec-term> -> <spec-term> ( is | =)
{ [ <sm-rules>] }
<sm-rules> -> <sm-rule> (, <sm-rule>)*
<sm-rule> -> <sort-or-op-ref> -> <sort-or-op-ref>
<sort-or-op-ref> -> <qualified-name> | ( <qualified-name>: <spec-sort-term> )
Specification Morphism Terms
<sm-term> -> <sm-ref> | <local-signature-morphism> | <sm-operation>
<sm-ref> -> <symbol>
<local-signature-morphism> ->
[morphism <spec-term>-> <spec-term>] { [<sm-rules>] }
<sm-operation> ->
identity-morphism | translation-morphism |
import-morphism | cocone-morphism from <symbol>
Diagrams
<global-sm-diagram> ->
diagram <symbol> (is | =)
[ nodes <sm-node> (, <sm-node>) *]
[ arcs <sm-arc> (, <sm-arc> )*]
end-diagram
Diagram Terms
<diagram-term> -> <diagram-ref> | <local-sm-diagram>
<diagram-ref> -> <symbol>
<local-sm-diagram> ->
diagram
[nodes <sm-node> ( , <sm-node> )*]
[arcs <sm-arc> ( , <sm-arc> )* ]
end-diagram
Diagram Elements
<sm-node> -> [ <symbol> : ] <spec-term>
<sm-arc> -> [ <symbol> : ] <sm-node-ref> -> <sm-node-ref> : <sm-term>
<sm-node-ref> -> <symbol>
Qualified Names
<qualified-name> -> (<node-name> . )* s<sort-or-op-name>
<node-name> -> <symbol>
<sort-or-op-name> -> <symbol>
Simple Name
<symbol> -> <symbol-start-char> <symbol-continue-char> *
<symbol-start-char> \xce
*abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ
<symbol-continue-char> \xce
-*abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ
1234567890?!
Comments
The character ``%'' indicates the start of a comment; everything which follows until the end of the line is ignored. Larger pieces of text can be commented out by enclosing them in ``#||...||#''; these characters function as brackets and can be nested.
B.3 Refinement Constructs
In addition to specifications, morphisms, and diagrams, there are two additional top-level constructs in Slang: interpretation schemes and interpretation scheme morphisms.
<top-level-slang-object> -> <global-ip-scheme> | <global-ips-morphism>
Interpretations and Interpretation Schemes
<global-ip-scheme> ->
(interpretation | ip-scheme) <symbol> : <spec-term> => <spec-term> ( is | =)
mediator <spec-term>
( dom-to-med | domain-to-mediator) <sm-term>
( cod-to-med | codomain-to-mediator) <sm-term>
Interpretation (Scheme) Terms
<ips-term> -> <ips-ref> | <local-ip-scheme>
<ips-ref> -> <symbol>
<local-ip-scheme> ->
(interpretation | ip-scheme) [ <spec-term> = | <spec-term>]
mediator <spec-term>
(dom-to-med | domain-to-mediator) <sm-term>
(cod-to-med | codomain-to-mediator) <sm-term>
Interpretation (Scheme) Morphisms
<global-ips-morphism> ->
ip-scheme-morphism <symbol>: <ips-term> -> <ips-term> (is| =)
domain-sm <sm-term>
mediator-sm <sm-term>
codomain-sm <sm-term>
Interpretation (Scheme) Morphism Terms
<ipsm-term> -> <ipsm-ref> | <local-ips-morphism>
ipsm-ref> -> <symbol>
<local-ips-morphism> ->
ip-scheme-morphism
domain-sm <sm-term>
mediator-sm <sm-term>
codomain-sm <sm-term>
C Table of Terms
The following table summarizes the construction of terms in Slang, and their sorts.
D Example: Nonnegative Integers
In Section 1, page 4, we saw a basic specification NAT-BASIC for the nonnegative integers. While that specification does describe the set of nonnegative integers, it does not provide definitions for many of the functions and relations we would expect in such a theory, such as addition, multiplication, and the ordering relations.
The following specification NAT, a definitional extension of NAT-BASIC, introduces some of the operations we need, including a predecessor function, addition, and the less-than and less-than-or-equal-to relations.
spec NAT is
import NAT-BASIC
op pred : Pos -> Nat
definition of pred is
axiom (equal (pred (succ x)) x)
end-definition
op plus : Nat, Nat -> Nat
definition of plus is
axiom (equal (plus zero y) y)
axiom (equal (plus (nat-of-pos (succ x)) y)
(nat-of-pos (succ (plus x y))))
end-definition
op leq : Nat, Nat -> Boolean
definition of leq is
axiom (iff (leq x zero) (equal x zero))
axiom (iff (leq x ((relax nonzero?) (succ y)))
(or (leq x y)
(equal x ((relax nonzero?) (succ y)))))
end-definition
op lt : Nat, Nat -> Boolean
definition of lt is
axiom (iff (lt x y)
(and (leq x y)
(not (equal x y))))
end-definition
theorem (equal (plus zero y) y)
theorem associativity-of-plus is
(equal (plus x (plus y z)) (plus (plus x y) z))
theorem commutativity-of-plus is
(equal (plus x y) (plus y x))
end-spec
This specification does define a predecessor function pred, the addition function plus, and the ordering relations leq and lt. This is enough to participate in the specification for arrays, which appears in the following section. It still does not define such common operations as multiplication, exponentiation, the divides relation, or the constant one, which are in the library version of the specification for the nonnegative integers.
E Example: Sequences into Arrays
In this appendix we present full specifications for arrays and describe the refinement from basic sequences into arrays. These were discussed in Example 5.4, page 73. We build on the more complete specification NAT from the previous appendix (Section D), rather than the basic specification NAT-BASIC given in Section 1. This is because we need the less-than relation lt, which is only defined in NAT.
We distinguish between static and dynamic arrays.
E.1 Static Arrays
The specification for static arrays is as follows:
spec ARRAY is
import NAT
sorts E, Array, Array-and-Interval
op make-array : Nat, E -> Array
op size-array : Array -> Nat
op in-bounds? : Array, Nat -> Boolean
definition of in-bounds? is
axiom (iff (in-bounds? a i) (lt i (size-array a)))
end-definition
sort-axiom Array-and-Interval = (Array, Nat) | in-bounds?
op access-array : Array-and-Interval -> E
axiom access-of-make-array is
(implies (and (equal a (make-array n e))
(equal ((relax in-bounds?) a-and-i) <a i>))
(equal (access-array a-and-i) e))
axiom size-of-make-array is
(equal (size-array (make-array n e)) n)
op update-array : Array-and-Interval, E -> Array
axiom access-of-update-same is
(implies
(and (equal ((relax in-bounds?) a-and-i) <a i>)
(equal ((relax in-bounds?) upi-and-i)
<(update-array a-and-i e) i>))
(equal (access-array upi-and-i) e))
axiom access-of-update-distinct is
(implies
(and (not (equal i j))
(and (equal ((relax in-bounds?) a-and-i) <a i>)
(and (equal ((relax in-bounds?) a-and-j) <a j>)
(equal ((relax in-bounds?) upi-and-j)
<(update-array a-and-i e) j>))))
(equal (access-array upi-and-j)
(access-array a-and-j)))
axiom size-of-update-array is
(implies
(equal ((relax in-bounds?) a-and-i) <a i>)
(equal (size-array (update-array a-and-i e))
(size-array a)))
axiom equal-array is
(iff (equal a1 a2)
(and (equal (size-array a1) (size-array a2))
(fa (i)
(implies
(and (equal ((relax in-bounds?) a1-and-i) <a1 i>)
(equal ((relax in-bounds?) a2-and-i) <a2 i>))
(equal (access-array a1-and-i)
(access-array a2-and-i))))))
constructors {make-array, update-array} construct Array
end-spec
Note that certain array operations are defined only for indices that are within the bounds of the array. For instance, access-array, the function that returns the ith element of the array a, is not defined on all arrays and nonnegative integers, but only on a pair a-and-i consisting of an array a and a nonnegative index i less than the size of a. The domain of this operation is thus a subsort of the product sort (Array, Nat), those pairs that satisfy a predicate in-bounds?. Applying the operator (relax in-bounds?) to the subsort element a-and-i yields the corresponding pair <a i>. Therefore, a statement such as
(equal ((relax in-bounds?) a-and-i) <a i>)
can be understood to say that i is a nonnegative index within the bounds of the array a, and that a-and-i is the element of the domain subsort corresponding to the pair <a i>.
The function (make-array n e) constructs an initial array of size n, each of whose elements is initialized to e. According to the axiom access-of-make-array, the ith element of this array must be e, for any index i that is within bounds. According to the axiom size-of-make-array, the size of this array is indeed n.
The function (update-array a-and-i e) assigns the ith element of array a to be e, where i is within bounds and a-and-i is the element of the domain subsort corresponding to a and i. The axiom access-of-update-same says that the ith element of the updated array will be e. The axiom access-of-update-distinct says that the jth element of the updated array will be the same as the jth element of the original array a, if j is within bounds and is distinct from i.
The equality axiom equal-array asserts that two arrays are equal if they have the same size and their corresponding elements are equal. The constructor set, which corresponds to an induction axiom, says that any array can be constructed by first making an initial array (all of whose elements are the same) and then applying a series of update operations.
E.2 Dynamic Arrays
Dynamic arrays are a definitional extension of static arrays that allow an array to be enlarged so that a new element can be introduced at the end.
spec DYNAMIC-ARRAY is
import ARRAY
const empty-array : Array
definition of empty-array is
axiom (equal empty-array (make-array zero e))
end-definition
op extend-array : Array, E -> Array
definition of extend-array is
axiom access-of-extend-array-last is
(implies
(equal ((relax in-bounds?) exa-and-s)
<(extend-array a e) (size-array a)>)
(equal (access-array exa-and-s)
e))
axiom access-of-extend-array is
(implies
(and (equal ((relax in-bounds?) a-and-i) <a i>)
(equal ((relax in-bounds?) exa-and-i)
<(extend-array a e) i>))
(equal (access-array exa-and-i)
(access-array a-and-i)))
axiom size-of-extend-array is
(equal (size-array (extend-array a e))
((relax nonzero?) (succ (size-array a))))
end-definition
constructors {empty-array, extend-array} construct Array
end-spec
The constant empty-array is the array of size 0, with no elements. According to its definition, it is equal to the result of constructing an initial array of size 0; it doesn't matter what element e the array elements are initialized to, since there are none. This constant could have been defined for the static arrays, but we didn't need it there; here it is part of the constructor set. It will also serve as the implementation for the empty sequence.
The function (extend-array a e) adds a new element e to the end of the array a. According to the axiom access-of-extend-array-last, the last element of this extended array will be e. According to the axiom access-of-extend-array, the ith element of the extended array will be the same as the ith element of the original array a, if i is within the bounds of a. Finally, according to the axiom size-of-extend-array, the size of the extended array is one greater than the size of the original array.
The constructor set, which corresponds to an induction axiom, says that any array can be constructed by successively extending the empty array. This axiom is logically redundant--it follows from the induction axiom corresponding to the constructor set for static arrays. Many proofs, however, are significantly easier using the new induction axiom.
E.3 Sequences as Arrays
The specification SEQ-AS-ARRAY is a definitional extension of DYNAMIC-ARRAY that contains implementations for the basic sequence specification. It serves as the mediator for the interpretation of basic sequences as arrays.
spec SEQ-AS-ARRAY is
import translate DYNAMIC-ARRAY
by {empty-array -> empty-s-as-a}
op prepend-s-as-a : E, Array -> Array
definition of prepend-s-as-a is
axiom (equal
(prepend-s-as-a e a)
(extend-array a e))
end-definition
constructors {empty-s-as-a, prepend-s-as-a} construct Array
end-spec
E.4 Sequences into Arrays
The interpretation from basic sequences into arrays is as follows:
interpretation SEQ-BASIC-TO-ARRAY : SEQ-BASIC => ARRAY is
mediator SEQ-AS-ARRAY
dom-to-med {Seq -> Array,
empty-seq -> empty-s-as-a,
prepend -> prepend-s-as-a}
cod-to-med import-morphism
The empty sequence is represented as the empty array. The function prepend for sequences is defined in terms of the function extend-array of dynamic arrays.
F Example: Finite Sets into Fixed Bit Vectors
In this appendix we present the full specification for fixed bit vectors and describe the refinement of finite sets into fixed bit vectors. These were discussed in Example 5.20.
F.1 Bits, Bit Vectors, and Fixed Bit Vectors
Here is the specification for bits:
spec BIT is
sort Bit
op zero : Bit
op one : Bit
axiom (not (equal zero one))
constructors {zero, one} construct Bit
end-spec
Bit vectors are arrays of bits:
spec BIT-VECTOR is
colimit of
diagram
nodes ONE-SORT, ARRAY, BIT
arcs ONE-SORT -> ARRAY : {X -> E},
ONE-SORT -> BIT : {X -> Bit}
end-diagram
We augment the specification for bit vectors to describe bit vectors all of the same size, size-vector.
spec BIT-VECTOR-FIXED is
import BIT-VECTOR
const size-vector : Nat
sort Interval
sort-axiom Interval = Nat | in-interval?
op in-interval? : Nat -> Boolean
definition of in-interval? is
axiom (iff (in-interval? i)
(lt i size-vector))
end-definition
sort Bit-Vector-Fixed
sort-axiom Bit-Vector-Fixed = Array | of-given-size?
op of-given-size? : Array -> Boolean
definition of of-given-size? is
axiom (iff (of-given-size? a)
(equal (size-array a) size-vector))
end-definition
op make-bvf : Bit -> Bit-Vector-Fixed
definition of make-bvf is
axiom (equal ((relax of-given-size?) (make-bvf b))
(make-array size-vector b))
end-definition
op update-bvf : Bit-Vector-Fixed, Interval, Bit
-> Bit-Vector-Fixed
definition of update-bvf is
axiom (implies
(equal ((relax in-bounds?) v-and-i)
<((relax of-given-size?) v)
((relax in-interval?) i)>)
(equal
((relax of-given-size?) (update-bvf v i b))
(update-array v-and-i b)))
end-definition
op access-bvf : Bit-Vector-Fixed, Interval -> Bit
definition of access-bvf is
axiom (implies
(equal ((relax in-bounds?) v-and-i)
<((relax of-given-size?) v)
((relax in-interval?) i)>)
(equal
(access-bvf v i)
(access-array v-and-i)))
end-definition
end-spec
Because in this specification all bit vectors are the same length, we do not have to have to introduce a subsort of the pairs to serve as the domain for the vector operations access-bvf and update-bvf. We introduce a subsort Interval of the nonnegative integers, those less than size-vector, to serve as the sort for the indices. The fixed bit vectors themselves are a subsort Bit-Vector-Fixed of the arrays, those of size equal to size-vector. Thus, access-bvf is defined over the entire product
(Bit-Vector-Fixed, Interval)
The axioms relate the functions on fixed bit vectors with the corresponding functions on arrays. The relax operator is used to map objects in subsorts with their counterparts in the corresponding supersorts.
F.2 Sets as Fixed Bit Vectors
This specification augments fixed bit vectors to mimic set operations. It serves as the mediator of the interpretation from finite sets into fixed bit vectors.
spec SET-AS-BIT-VECTOR-FIXED is
import BIT-VECTOR-FIXED
const empty-s-as-bvf : Bit-Vector-Fixed
definition of empty-s-as-bvf is
axiom (equal empty-s-as-bvf (make-bvf BIT.zero))
end-definition
op insert-s-as-bvf : Interval, Bit-Vector-Fixed
-> Bit-Vector-Fixed
definition of insert-s-as-bvf is
axiom (equal (insert-s-as-bvf i v)
(update-bvf v i BIT.one))
end-definition
op in-s-as-bvf? : Interval, Bit-Vector-Fixed -> Boolean
definition of in-s-as-bvf? is
axiom (iff (in-s-as-bvf? i v)
(equal (access-bvf v i) BIT.one))
end-definition
constructors {empty-s-as-bvf, insert-s-as-bvf} construct
Bit-Vector-Fixed
end-spec
It is described on page 77.
F.3 Finite Sets into Fixed Bit Vectors
Here is the interpretation of finite sets into fixed bit vectors.
interpretation SET-TO-BIT-VECTOR-FIXED :
SET => BIT-VECTOR-FIXED is
mediator SET-AS-BIT-VECTOR-FIXED
dom-to-med
{E -> Interval,
Set -> Bit-Vector-Fixed,
empty-set -> empty-s-as-bvf,
insert-set -> insert-s-as-bvf,
in-set? -> in-s-as-bvf?}
cod-to-med import-morphism
G Example: Bags into Bags via a Quotient
In this appendix we present an interpretation scheme of bags into bags. This scheme is intended to be applied as one component of a parallel refinement. The sort of the elements of the bags in this component is identified with a sort in another component, and that sort is mapped into a quotient modulo an undefined equivalence relation. For instance, in the example Bags of Bags (Example 5.23), the elements of the bags in this component are identified with the inner bags in another component, and the inner bags are mapped into a quotient of sequences modulo the permutation relation.
The interpretation scheme that fulfills this role is as follows:
interpretation BAG-VIA-QUOTIENT : BAG => BAG is
mediator BAG-QUOTIENT
dom-to-med BAG-TO-Q-BAG
cod-to-med BAG-TO-B-BAG
Here the source morphism is
morphism BAG-TO-Q-BAG : BAG -> BAG-QUOTIENT is
{Bag -> Q.Bag,
E -> Q,
empty-bag -> Q.empty-bag,
insert-bag -> Q.insert-bag,
in-bag? -> Q.in-bag?}
The mediator BAG-QUOTIENT has two copies of the theory of bags, the B-bags and the Q-bags, with elements of sorts B and Q respectively. The sort Q is a quotient of B modulo r?, where r? is an equivalence relation on B.
The source morphism BAG-TO-Q-BAG maps the element sort E in the domain bag into the sort Q in the mediator. The bag sorts and operations in the domain are mapped into sorts and operations on Q-bags in the mediator. The target morphism BAG-TO-B-BAG is analogous--it maps sorts and operations on bags in the codomain into sorts and operations on B-bags in the mediator.
Because the equivalence relation r? is not defined, the target morphism is not a definitional extension, and the ip-scheme fails to be a full-fledged interpretation. Definitions in the mediator express the other operations on Q-bags in terms of operations on B-bags.
The mediator BAG-QUOTIENT is as follows:
spec BAG-QUOTIENT is
import
translate
colimit of
diagram
nodes B : BAG, Q : BAG
end-diagram
by {B.E -> B,
Q.E -> Q}
op r? : B, B -> Boolean
sort-axiom Q = B/r?
op subbag-mod-r? : B.Bag, B.Bag -> Boolean
definition of subbag-mod-r? is
axiom (subbag-mod-r? B.empty-bag bb2)
axiom (iff (subbag-mod-r? (B.insert-bag b1 bb1) b2-bb2)
(ex (b2 bb2)
(and (equal b2-bb2 (B.insert-bag b2 bb2))
(and (r? b1 b2)
(subbag-mod-r? bb1 bb2)))))
end-definition
op eq-bag-mod-r? : B.Bag, B.Bag -> Boolean
definition of eq-bag-mod-r? is
axiom (iff (eq-bag-mod-r? bb1 bb2)
(and (subbag-mod-r? bb1 bb2)
(subbag-mod-r? bb2 bb1)))
end-definition
sort-axiom Q.Bag = B.Bag/eq-bag-mod-r?
definition of Q.empty-bag is
axiom (equal Q.empty-bag ((quotient eq-bag-mod-r?) B.empty-bag))
end-definition
definition of Q.insert-bag is
axiom (equal (Q.insert-bag ((quotient r?) b)
(quotient eq-bag-mod-r?) bb))
((quotient eq-bag-mod-r?) (B.insert-bag b bb)))
end-definition
definition of Q.in-bag? is
axiom (iff (Q.in-bag? ((quotient r?) b)
((quotient eq-bag-mod-r?) bb))
(B.in-bag? b bb))
end-definition
constructors {B.empty-bag, B.insert-bag} construct B.Bag
constructors {Q.empty-bag, Q.insert-bag} construct Q.Bag
end-spec
The mediator provides auxiliary operations that allow us to define the Q-bag operations in terms of the B-bag operations. The predicate subbag-mod-r?(bb1,bb2) tests whether the B-bag bb1 is a subbag modulo r? of the bag bb2, i.e., whether there is a one-to-one mapping from bb1 into bb2 under which each element of bb1 corresponds to an equivalent element of bb2, where the equivalence is under the equivalence relation r?. For example, if B1 is equivalent to B2 modulo r?, the bag {{B1, B1}} is a subbag modulo r? of the bag {{B1, B2, B3}} but not of the bag {{B1, B3}}.
Note that the definition of subbag-mod-r? is not constructive (see Section 6.1). Not only is its format unacceptable for Specware's code generation, but also the existential quantifier does not in general describe a finite computation. If we were intending to generate code, we would have to rewrite it.
The predicate eq-bag-mod-r?(bb1,bb2} tests whether two B-bags are equal modulo r?, i.e., whether there exists a one-to-one correspondence between the two bags such that corresponding elements are equivalent modulo r?. For example, if B1 and B2 are equivalent modulo r?, the bag {{B1, B1, B3}} is equal modulo r? to the bag {{B1, B2, B3}} but not necessarily to the bag {{B1, B3, B3}}. In the definition, two B-bags are said to be equal modulo r? if each is a subbag of the other modulo r?.
The Q-bags, then, are defined to be the quotient of the B-bags modulo the relation eq-bag-mod-r?. The operations on Q-bags can then be defined in terms of the operations on B-bags, using the quotient function on the new relation eq-bag-mod-r?. Only r? is undefined.
Last Modified: 05:09pm PDT, June 24, 1996